Menu Close

find-lim-x-0-1-1-x-x-2-cos-2x-x-3-

Tinku Tara 0 Comments
Pin




Question Number 83019 by mathmax by abdo last updated on 27/Feb/20
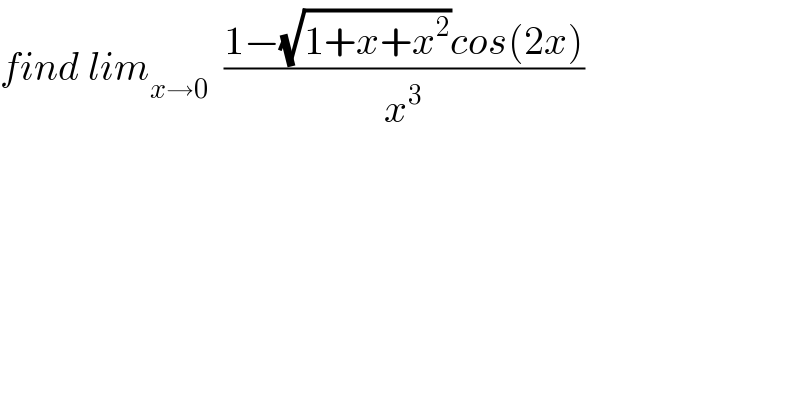
find lim_(x→0) ((1−(√(1+x+x^2 ))cos(2x))/x^3 )
$${find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{1}−\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }{cos}\left(\mathrm{2}{x}\right)}{{x}^{\mathrm{3}} } \\ $$
Commented by mathmax by abdo last updated on 27/Feb/20
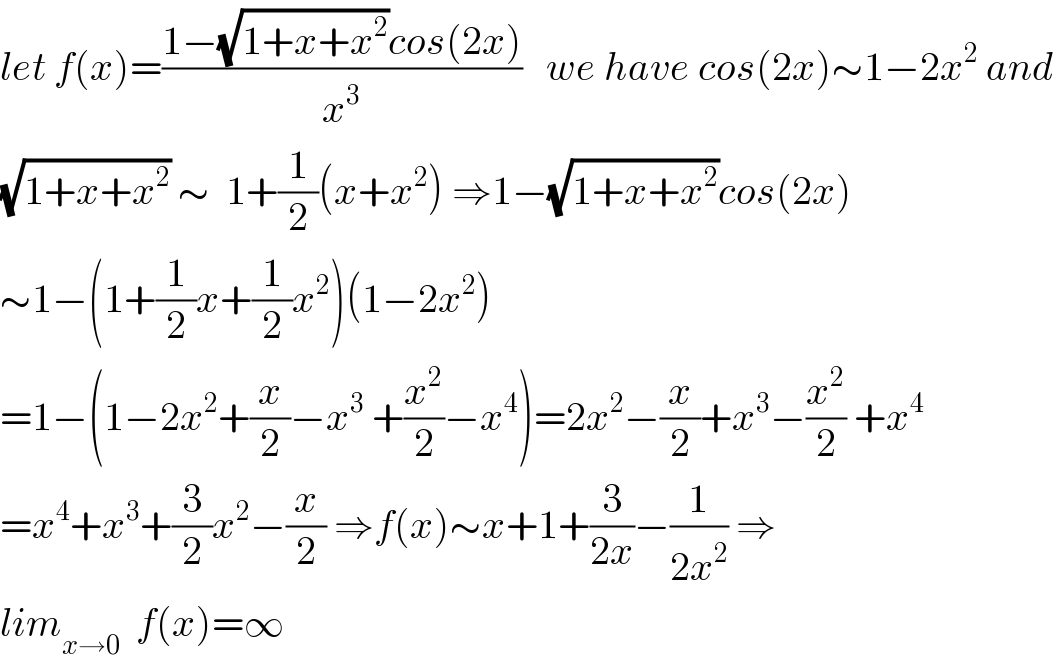
let f(x)=((1−(√(1+x+x^2 ))cos(2x))/x^3 ) we have cos(2x)∼1−2x^2 and (√(1+x+x^2 )) ∼ 1+(1/2)(x+x^2 ) ⇒1−(√(1+x+x^2 ))cos(2x) ∼1−(1+(1/2)x+(1/2)x^2 )(1−2x^2 ) =1−(1−2x^2 +(x/2)−x^3 +(x^2 /2)−x^4 )=2x^2 −(x/2)+x^3 −(x^2 /2) +x^4 =x^4 +x^3 +(3/2)x^2 −(x/2) ⇒f(x)∼x+1+(3/(2x))−(1/(2x^2 )) ⇒ lim_(x→0) f(x)=∞
$${let}\:{f}\left({x}\right)=\frac{\mathrm{1}−\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }{cos}\left(\mathrm{2}{x}\right)}{{x}^{\mathrm{3}} }\:\:\:{we}\:{have}\:{cos}\left(\mathrm{2}{x}\right)\sim\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \:{and} \\ $$$$\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }\:\sim\:\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left({x}+{x}^{\mathrm{2}} \right)\:\Rightarrow\mathrm{1}−\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }{cos}\left(\mathrm{2}{x}\right) \\ $$$$\sim\mathrm{1}−\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{x}+\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{1}−\left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} +\frac{{x}}{\mathrm{2}}−{x}^{\mathrm{3}} \:+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−{x}^{\mathrm{4}} \right)=\mathrm{2}{x}^{\mathrm{2}} −\frac{{x}}{\mathrm{2}}+{x}^{\mathrm{3}} −\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+{x}^{\mathrm{4}} \\ $$$$={x}^{\mathrm{4}} +{x}^{\mathrm{3}} +\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} −\frac{{x}}{\mathrm{2}}\:\Rightarrow{f}\left({x}\right)\sim{x}+\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}{x}}−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:{f}\left({x}\right)=\infty \\ $$
Answered by john santu last updated on 27/Feb/20
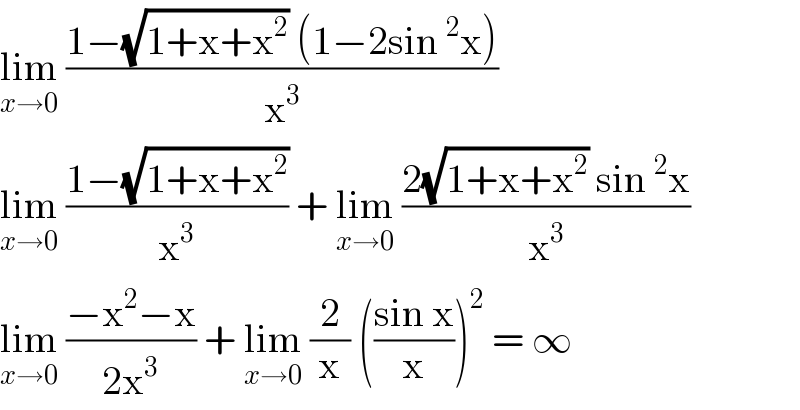
lim_(x→0) ((1−(√(1+x+x^2 )) (1−2sin^2 x))/x^3 ) lim_(x→0) ((1−(√(1+x+x^2 )))/x^3 ) + lim_(x→0) ((2(√(1+x+x^2 )) sin^2 x)/x^3 ) lim_(x→0) ((−x^2 −x)/(2x^3 )) + lim_(x→0) (2/x) (((sin x)/x))^2 = ∞
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} }\:\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{x}^{\mathrm{3}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}^{\mathrm{3}} }\:+\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{x}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{3}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{x}^{\mathrm{2}} −\mathrm{x}}{\mathrm{2x}^{\mathrm{3}} }\:+\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}}{\mathrm{x}}\:\left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\right)^{\mathrm{2}} \:=\:\infty\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *