Question Number 58530 by maxmathsup by imad last updated on 24/Apr/19
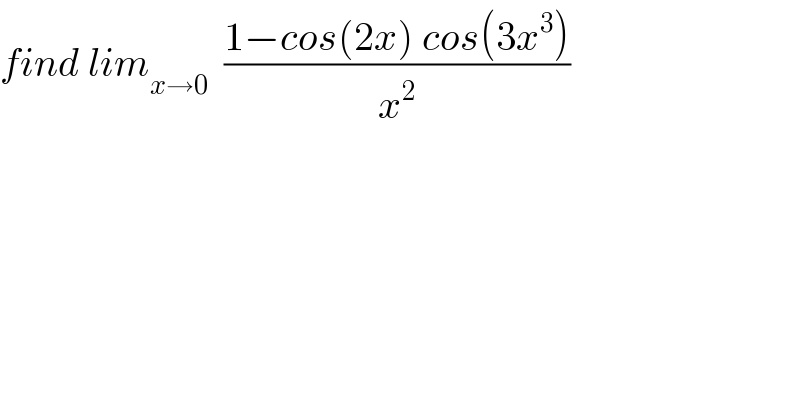
$${find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)\:{cos}\left(\mathrm{3}{x}^{\mathrm{3}} \right)}{{x}^{\mathrm{2}} } \\ $$
Answered by tanmay last updated on 24/Apr/19

$${cos}\mathrm{2}{x}=\mathrm{1}−\frac{\left(\mathrm{2}{x}\right)^{\mathrm{2}} }{\mathrm{2}!}+{others}\:{term}\:{ignored}\:{because} \\ $$$${those}\:{terms}\:{contain}\:{x}^{{r}} \:\:{when}\:{r}>\mathrm{2} \\ $$$${cos}\left(\mathrm{3}{x}^{\mathrm{3}} \right)=\mathrm{1}−\frac{\left(\mathrm{3}{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{\mathrm{2}!}+{others}\:{terms}\:{ignored} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left\{\left(\mathrm{1}−\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\mathrm{9}{x}^{\mathrm{6}} }{\mathrm{2}}\right)\right\}}{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{9}{x}^{\mathrm{6}} }{\mathrm{2}}−\mathrm{2}{x}^{\mathrm{2}} +\mathrm{9}{x}^{\mathrm{8}} \right)}{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{1}+\mathrm{2}{x}^{\mathrm{2}} +{others}\:{terms}\:{ignored}}{{x}^{\mathrm{2}} } \\ $$$$=\mathrm{2} \\ $$
Commented by malwaan last updated on 25/Apr/19
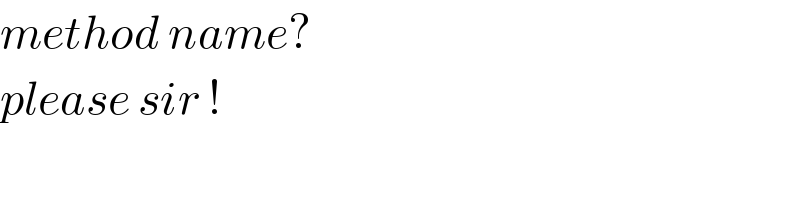
$${method}\:{name}? \\ $$$${please}\:{sir}\:! \\ $$
Commented by tanmay last updated on 25/Apr/19
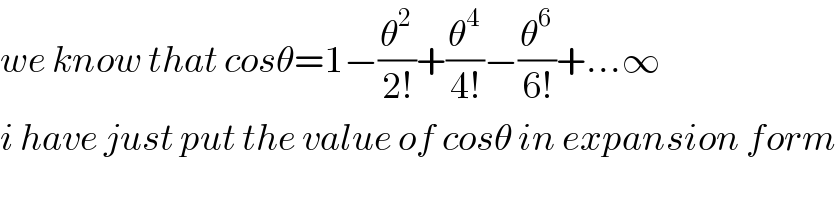
$${we}\:{know}\:{that}\:{cos}\theta=\mathrm{1}−\frac{\theta^{\mathrm{2}} }{\mathrm{2}!}+\frac{\theta^{\mathrm{4}} }{\mathrm{4}!}−\frac{\theta^{\mathrm{6}} }{\mathrm{6}!}+…\infty \\ $$$${i}\:{have}\:{just}\:{put}\:{the}\:{value}\:{of}\:{cos}\theta\:{in}\:{expansion}\:{form} \\ $$
Commented by maxmathsup by imad last updated on 25/Apr/19
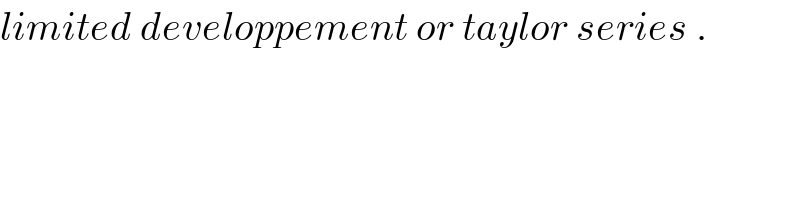
$${limited}\:{developpement}\:{or}\:{taylor}\:{series}\:. \\ $$
Commented by malwaan last updated on 27/Apr/19

$${thank}\:{you} \\ $$
Answered by kaivan.ahmadi last updated on 25/Apr/19
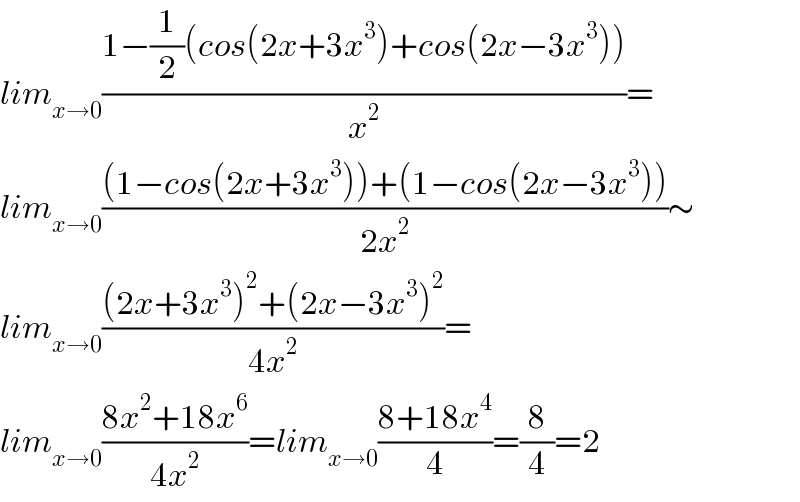
$${lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\left(\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{3}} \right)+{cos}\left(\mathrm{2}{x}−\mathrm{3}{x}^{\mathrm{3}} \right)\right)}{{x}^{\mathrm{2}} }= \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \frac{\left(\mathrm{1}−{cos}\left(\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{3}} \right)\right)+\left(\mathrm{1}−{cos}\left(\mathrm{2}{x}−\mathrm{3}{x}^{\mathrm{3}} \right)\right)}{\mathrm{2}{x}^{\mathrm{2}} }\sim \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \frac{\left(\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{3}} \right)^{\mathrm{2}} +\left(\mathrm{2}{x}−\mathrm{3}{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{2}} }= \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{8}{x}^{\mathrm{2}} +\mathrm{18}{x}^{\mathrm{6}} }{\mathrm{4}{x}^{\mathrm{2}} }={lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{8}+\mathrm{18}{x}^{\mathrm{4}} }{\mathrm{4}}=\frac{\mathrm{8}}{\mathrm{4}}=\mathrm{2} \\ $$
