Question Number 35726 by abdo mathsup 649 cc last updated on 22/May/18
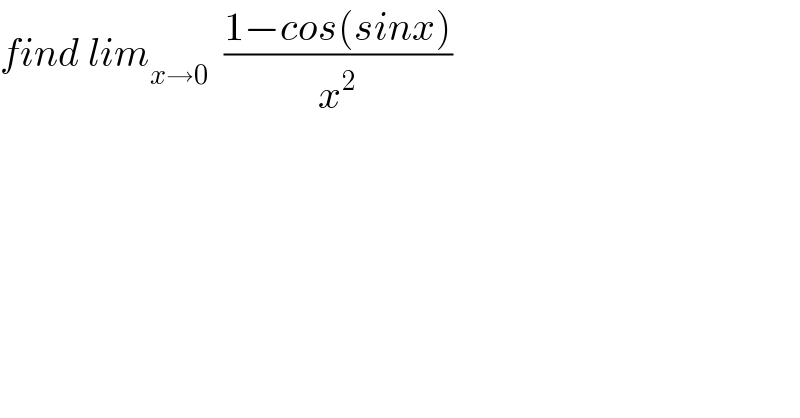
$${find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{1}−{cos}\left({sinx}\right)}{{x}^{\mathrm{2}} } \\ $$
Commented by abdo mathsup 649 cc last updated on 23/May/18
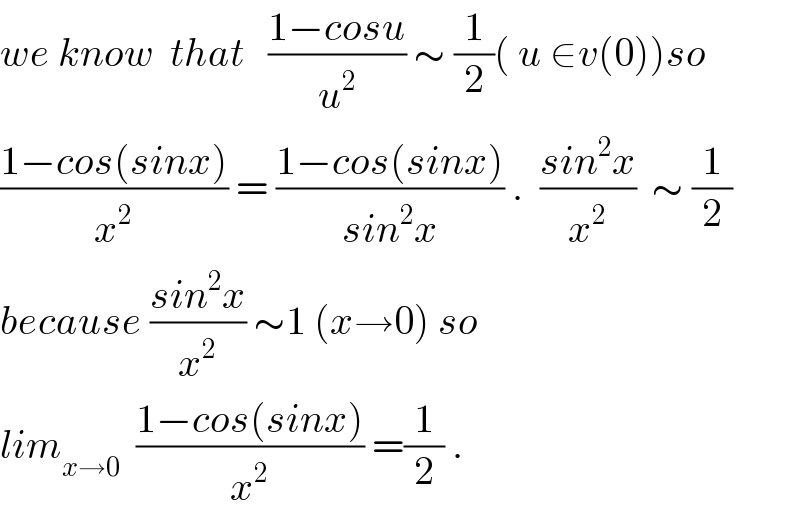
$${we}\:{know}\:\:{that}\:\:\:\frac{\mathrm{1}−{cosu}}{{u}^{\mathrm{2}} }\:\sim\:\frac{\mathrm{1}}{\mathrm{2}}\left(\:{u}\:\in{v}\left(\mathrm{0}\right)\right){so}\: \\ $$$$\frac{\mathrm{1}−{cos}\left({sinx}\right)}{{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}−{cos}\left({sinx}\right)}{{sin}^{\mathrm{2}} {x}}\:.\:\:\frac{{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }\:\:\sim\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${because}\:\frac{{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }\:\sim\mathrm{1}\:\left({x}\rightarrow\mathrm{0}\right)\:{so} \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{1}−{cos}\left({sinx}\right)}{{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$
Answered by $@ty@m last updated on 22/May/18
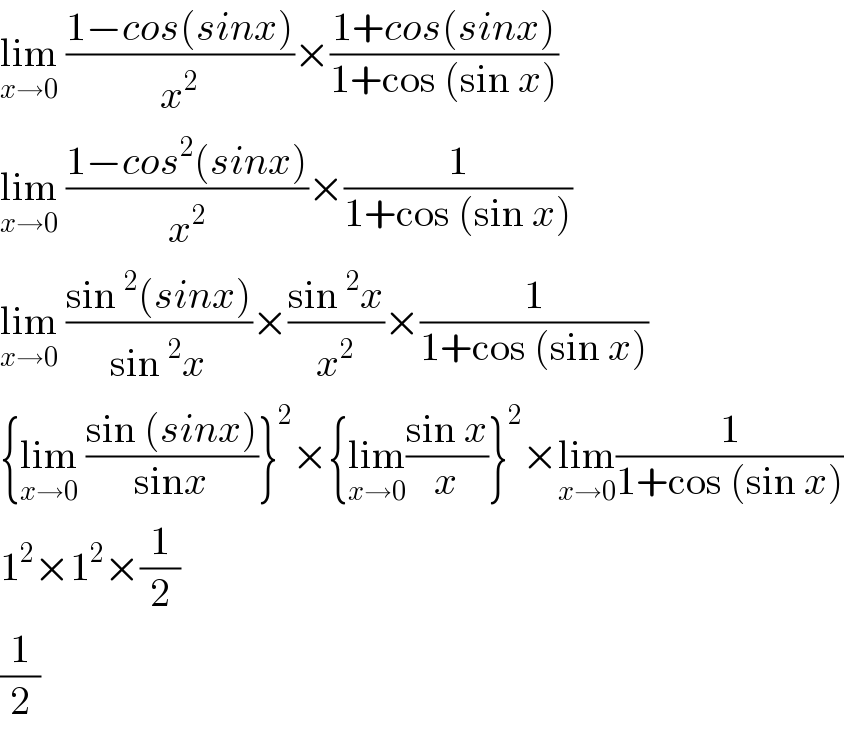
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−{cos}\left({sinx}\right)}{{x}^{\mathrm{2}} }×\frac{\mathrm{1}+{cos}\left({sinx}\right)}{\mathrm{1}+\mathrm{cos}\:\left(\mathrm{sin}\:{x}\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−{cos}^{\mathrm{2}} \left({sinx}\right)}{{x}^{\mathrm{2}} }×\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:\left(\mathrm{sin}\:{x}\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:^{\mathrm{2}} \left({sinx}\right)}{\mathrm{sin}\:^{\mathrm{2}} {x}}×\frac{\mathrm{sin}\:^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }×\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:\left(\mathrm{sin}\:{x}\right)} \\ $$$$\left\{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left({sinx}\right)}{\mathrm{sin}{x}}\right\}^{\mathrm{2}} ×\left\{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{x}}{{x}}\right\}^{\mathrm{2}} ×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:\left(\mathrm{sin}\:{x}\right)} \\ $$$$\mathrm{1}^{\mathrm{2}} ×\mathrm{1}^{\mathrm{2}} ×\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}} \\ $$
