Question Number 49800 by maxmathsup by imad last updated on 10/Dec/18
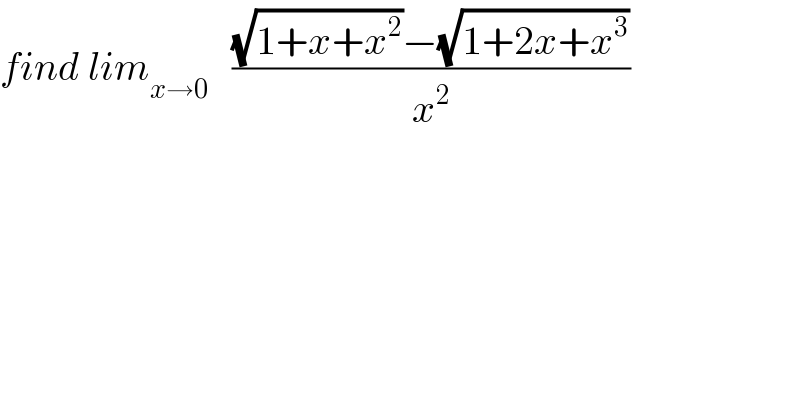
$${find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{\sqrt{\mathrm{1}+{x}+{x}^{\mathrm{2}} }−\sqrt{\mathrm{1}+\mathrm{2}{x}+{x}^{\mathrm{3}} }}{{x}^{\mathrm{2}} } \\ $$
Answered by afachri last updated on 12/Dec/18

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{\sqrt{{x}^{\mathrm{2}} +\:{x}\:+\:\mathrm{1}\:}\:\:−\:\:\sqrt{{x}^{\mathrm{3}} +\:\mathrm{2}{x}\:+\:\mathrm{1}\:}}{{x}^{\mathrm{2}} }\:\:.\:\:\frac{\sqrt{{x}^{\mathrm{2}} +\:{x}\:+\:\mathrm{1}\:}\:\:+\:\:\sqrt{{x}^{\mathrm{3}} +\:\mathrm{2}{x}\:+\:\mathrm{1}\:}}{\:\sqrt{{x}^{\mathrm{2}} +\:{x}\:+\:\mathrm{1}\:}\:\:+\:\:\sqrt{{x}^{\mathrm{3}} +\:\mathrm{2}{x}\:+\:\mathrm{1}\:}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\:\frac{\left({x}^{\mathrm{2}} +\:{x}\:+\:\mathrm{1}\right)\:−\:\left({x}^{\mathrm{3}} +\:\mathrm{2}{x}\:+\:\mathrm{1}\right)}{{x}^{\mathrm{2}} \left(\sqrt{{x}^{\mathrm{2}} +\:{x}\:+\:\mathrm{1}\:}\:\:+\:\:\sqrt{{x}^{\mathrm{3}} +\:\mathrm{2}{x}\:+\:\mathrm{1}\:}\:\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\:\frac{−{x}^{\mathrm{3}} +\:{x}^{\mathrm{2}} −\:{x}\:}{{x}^{\mathrm{2}} \left(\sqrt{{x}^{\mathrm{2}} +\:{x}\:+\:\mathrm{1}\:}\:\:+\:\:\sqrt{{x}^{\mathrm{3}} +\:\mathrm{2}{x}\:+\:\mathrm{1}\:}\:\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\:\frac{{x}^{\mathrm{2}} \left(−{x}\:+\:\mathrm{1}\:−\:\frac{\mathrm{1}}{{x}}\right)}{{x}^{\mathrm{2}} \left(\sqrt{{x}^{\mathrm{2}} +\:{x}\:+\:\mathrm{1}\:}\:\:+\:\:\sqrt{{x}^{\mathrm{3}} +\:\mathrm{2}{x}\:+\:\mathrm{1}\:}\:\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{−{x}\:+\:\mathrm{1}\:−\:\frac{\mathrm{1}}{{x}}\:}{\:\sqrt{{x}^{\mathrm{2}} +\:{x}\:+\:\mathrm{1}\:}\:\:+\:\:\sqrt{{x}^{\mathrm{3}} +\:\mathrm{2}{x}\:+\:\mathrm{1}\:}}\:\:=\:\:\infty \\ $$$$ \\ $$
