Question Number 90564 by mathmax by abdo last updated on 24/Apr/20

$${find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\frac{\left(^{\mathrm{3}} \sqrt{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}−\left(^{\mathrm{3}} \sqrt{\mathrm{2}}\right)\right.}{{x}^{\mathrm{2}} {sin}\left(\mathrm{3}{x}\right)} \\ $$
Commented by jagoll last updated on 25/Apr/20
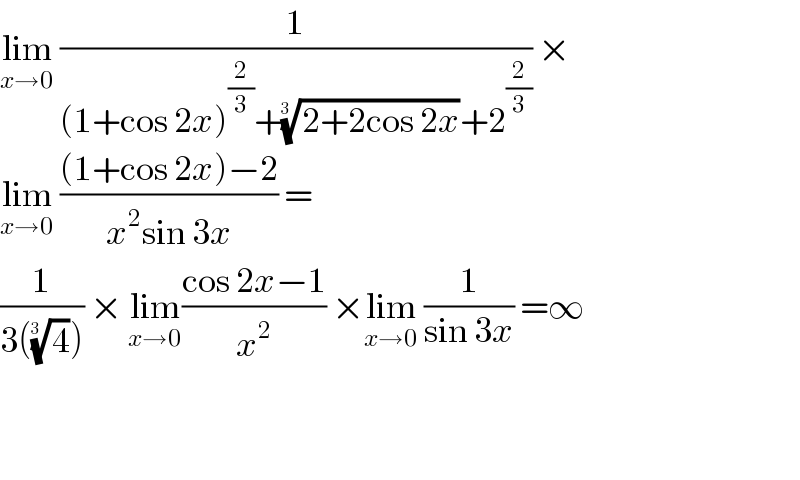
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} +\sqrt[{\mathrm{3}\:\:}]{\mathrm{2}+\mathrm{2cos}\:\mathrm{2}{x}}+\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:× \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}\right)−\mathrm{2}}{{x}^{\mathrm{2}} \mathrm{sin}\:\mathrm{3}{x}}\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{3}\left(\sqrt[{\mathrm{3}\:\:}]{\mathrm{4}}\right)}\:×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} }\:×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{3}{x}}\:=\infty \\ $$$$ \\ $$$$ \\ $$
