Question Number 110449 by mathmax by abdo last updated on 29/Aug/20

$$\mathrm{find}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\frac{\mathrm{arctan}\left(\mathrm{x}−\mathrm{sinx}\right)−\mathrm{arctan}\left(\mathrm{1}−\mathrm{cosx}\right)}{\mathrm{x}^{\mathrm{2}} } \\ $$
Answered by bemath last updated on 29/Aug/20
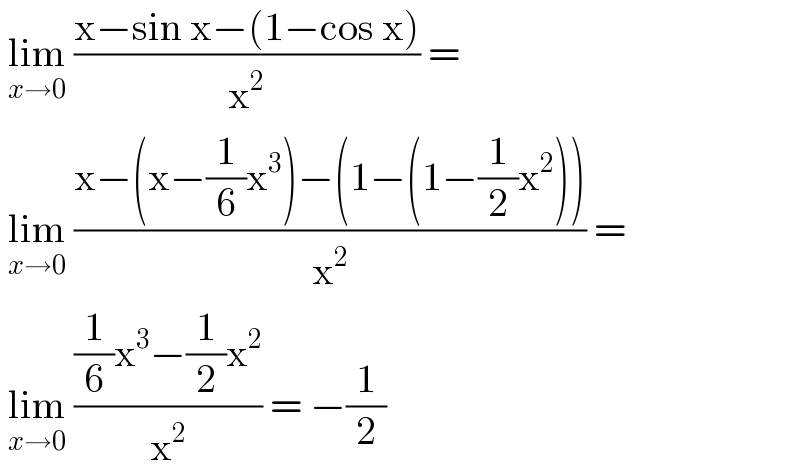
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}−\left(\mathrm{1}−\mathrm{cos}\:\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} }\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}−\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} \right)−\left(\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \right)\right)}{\mathrm{x}^{\mathrm{2}} }\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 29/Aug/20
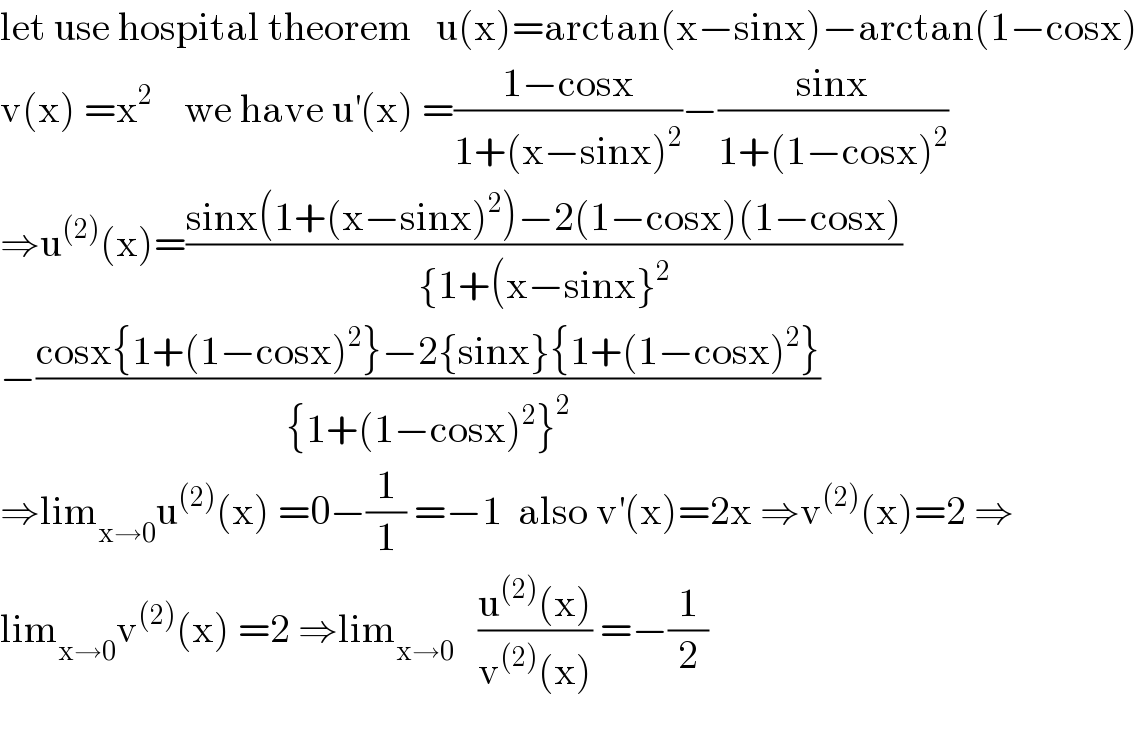
$$\mathrm{let}\:\mathrm{use}\:\mathrm{hospital}\:\mathrm{theorem}\:\:\:\mathrm{u}\left(\mathrm{x}\right)=\mathrm{arctan}\left(\mathrm{x}−\mathrm{sinx}\right)−\mathrm{arctan}\left(\mathrm{1}−\mathrm{cosx}\right) \\ $$$$\mathrm{v}\left(\mathrm{x}\right)\:=\mathrm{x}^{\mathrm{2}} \:\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{u}^{'} \left(\mathrm{x}\right)\:=\frac{\mathrm{1}−\mathrm{cosx}}{\mathrm{1}+\left(\mathrm{x}−\mathrm{sinx}\right)^{\mathrm{2}} }−\frac{\mathrm{sinx}}{\mathrm{1}+\left(\mathrm{1}−\mathrm{cosx}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{u}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)=\frac{\mathrm{sinx}\left(\mathrm{1}+\left(\mathrm{x}−\mathrm{sinx}\right)^{\mathrm{2}} \right)−\mathrm{2}\left(\mathrm{1}−\mathrm{cosx}\right)\left(\mathrm{1}−\mathrm{cosx}\right)}{\left\{\mathrm{1}+\left(\mathrm{x}−\mathrm{sinx}\right\}^{\mathrm{2}} \right.} \\ $$$$−\frac{\mathrm{cosx}\left\{\mathrm{1}+\left(\mathrm{1}−\mathrm{cosx}\right)^{\mathrm{2}} \right\}−\mathrm{2}\left\{\mathrm{sinx}\right\}\left\{\mathrm{1}+\left(\mathrm{1}−\mathrm{cosx}\right)^{\mathrm{2}} \right\}}{\left\{\mathrm{1}+\left(\mathrm{1}−\mathrm{cosx}\right)^{\mathrm{2}} \right\}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{u}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)\:=\mathrm{0}−\frac{\mathrm{1}}{\mathrm{1}}\:=−\mathrm{1}\:\:\mathrm{also}\:\mathrm{v}^{'} \left(\mathrm{x}\right)=\mathrm{2x}\:\Rightarrow\mathrm{v}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)=\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{v}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)\:=\mathrm{2}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{u}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)}{\mathrm{v}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)}\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
