Question Number 33313 by abdo imad last updated on 14/Apr/18
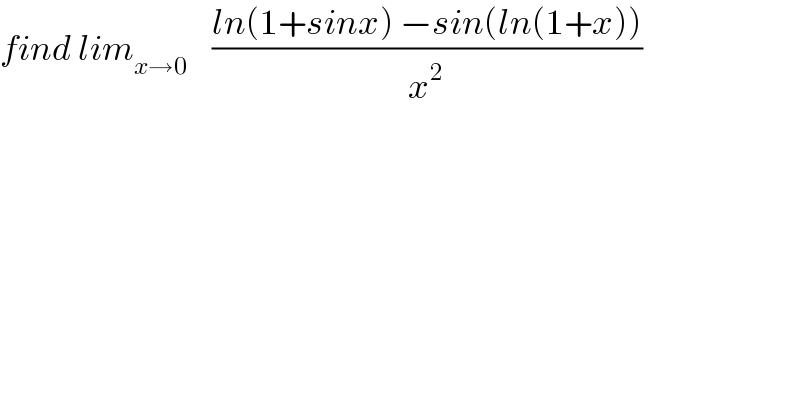
$${find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\frac{{ln}\left(\mathrm{1}+{sinx}\right)\:−{sin}\left({ln}\left(\mathrm{1}+{x}\right)\right)}{{x}^{\mathrm{2}} } \\ $$
Commented by abdo imad last updated on 17/Apr/18
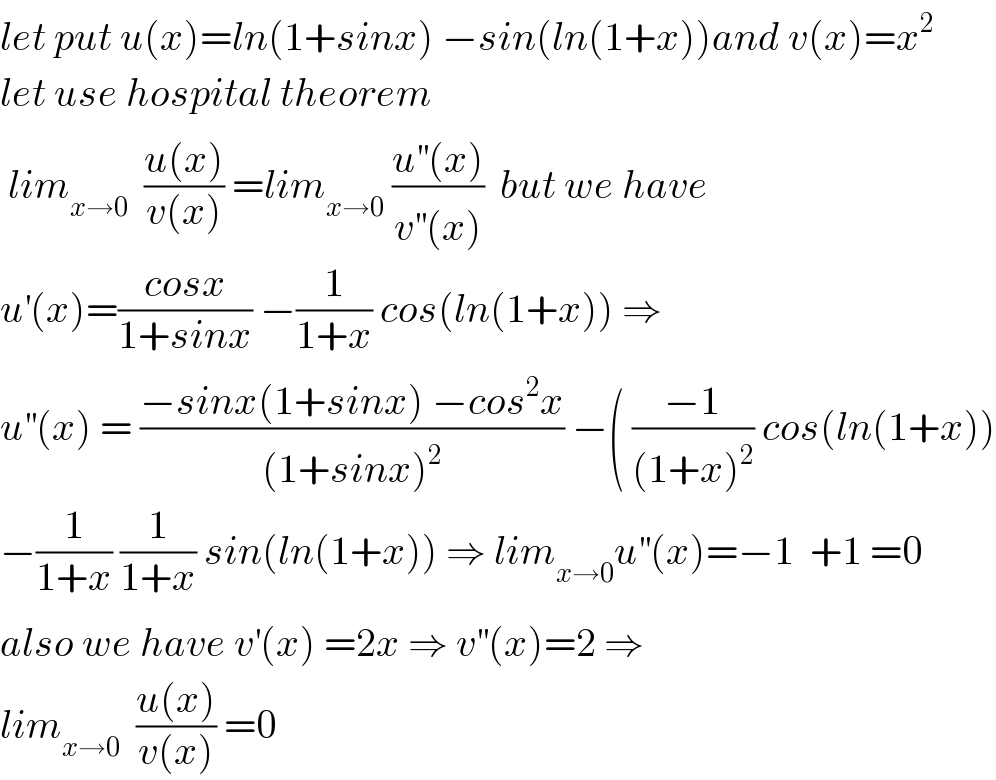
$${let}\:{put}\:{u}\left({x}\right)={ln}\left(\mathrm{1}+{sinx}\right)\:−{sin}\left({ln}\left(\mathrm{1}+{x}\right)\right){and}\:{v}\left({x}\right)={x}^{\mathrm{2}} \\ $$$${let}\:{use}\:{hospital}\:{theorem} \\ $$$$\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{{u}\left({x}\right)}{{v}\left({x}\right)}\:={lim}_{{x}\rightarrow\mathrm{0}} \:\frac{{u}^{''} \left({x}\right)}{{v}^{''} \left({x}\right)}\:\:{but}\:{we}\:{have} \\ $$$${u}^{'} \left({x}\right)=\frac{{cosx}}{\mathrm{1}+{sinx}}\:−\frac{\mathrm{1}}{\mathrm{1}+{x}}\:{cos}\left({ln}\left(\mathrm{1}+{x}\right)\right)\:\Rightarrow \\ $$$${u}^{''} \left({x}\right)\:=\:\frac{−{sinx}\left(\mathrm{1}+{sinx}\right)\:−{cos}^{\mathrm{2}} {x}}{\left(\mathrm{1}+{sinx}\right)^{\mathrm{2}} }\:−\left(\:\frac{−\mathrm{1}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }\:{cos}\left({ln}\left(\mathrm{1}+{x}\right)\right)\right. \\ $$$$−\frac{\mathrm{1}}{\mathrm{1}+{x}}\:\frac{\mathrm{1}}{\mathrm{1}+{x}}\:{sin}\left({ln}\left(\mathrm{1}+{x}\right)\right)\:\Rightarrow\:{lim}_{{x}\rightarrow\mathrm{0}} {u}^{''} \left({x}\right)=−\mathrm{1}\:\:+\mathrm{1}\:=\mathrm{0} \\ $$$${also}\:{we}\:{have}\:{v}^{'} \left({x}\right)\:=\mathrm{2}{x}\:\Rightarrow\:{v}^{''} \left({x}\right)=\mathrm{2}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{{u}\left({x}\right)}{{v}\left({x}\right)}\:=\mathrm{0} \\ $$
