Menu Close

find-lim-x-0-ln-sin-3x-cos-3x-ln-sin-x-cos-x-

Tinku Tara 0 Comments
Pin




Question Number 88896 by M±th+et£s last updated on 13/Apr/20
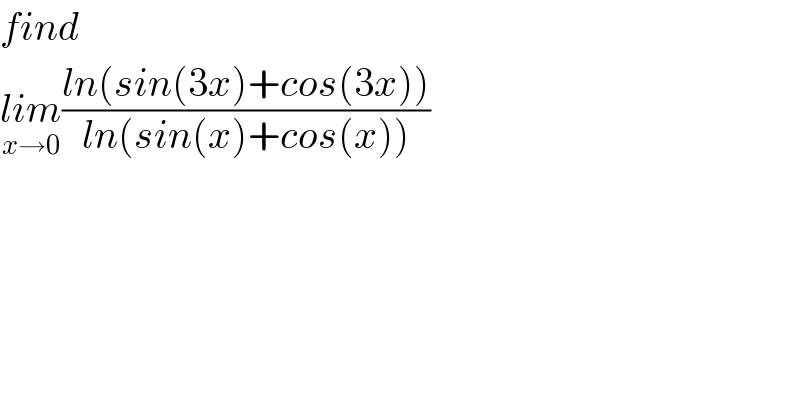
find lim_(x→0) ((ln(sin(3x)+cos(3x)))/(ln(sin(x)+cos(x))))
$${find}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{ln}\left({sin}\left(\mathrm{3}{x}\right)+{cos}\left(\mathrm{3}{x}\right)\right)}{{ln}\left({sin}\left({x}\right)+{cos}\left({x}\right)\right)} \\ $$
Commented by abdomathmax last updated on 13/Apr/20
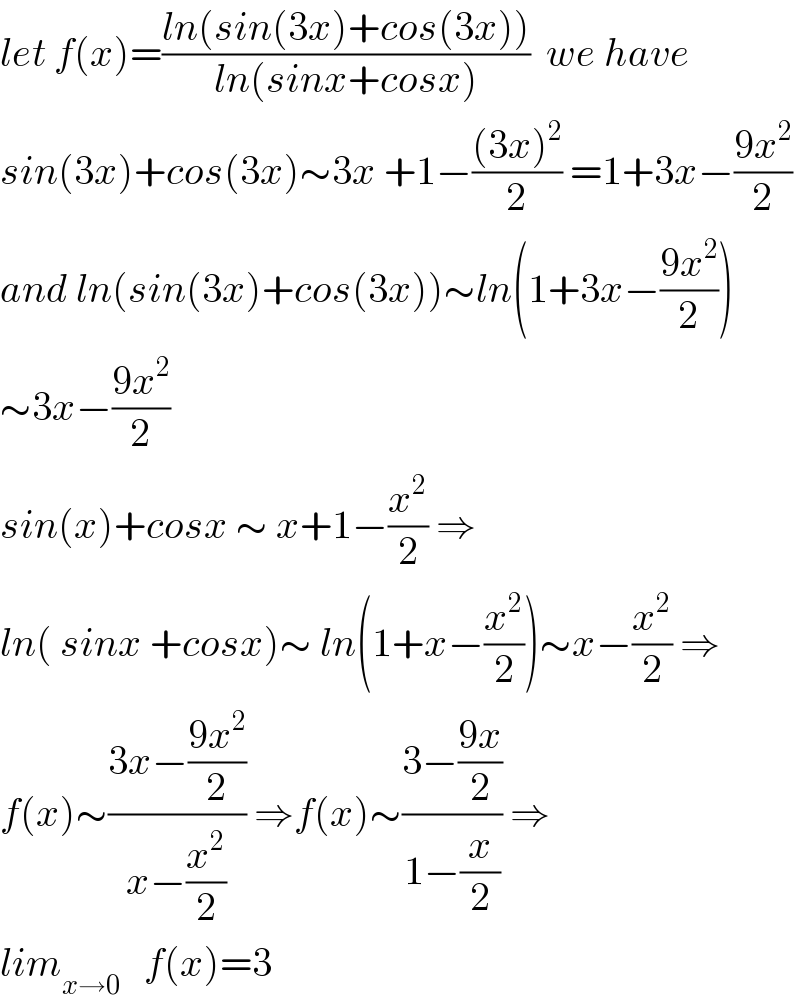
let f(x)=((ln(sin(3x)+cos(3x)))/(ln(sinx+cosx))) we have sin(3x)+cos(3x)∼3x +1−(((3x)^2 )/2) =1+3x−((9x^2 )/2) and ln(sin(3x)+cos(3x))∼ln(1+3x−((9x^2 )/2)) ∼3x−((9x^2 )/2) sin(x)+cosx ∼ x+1−(x^2 /2) ⇒ ln( sinx +cosx)∼ ln(1+x−(x^2 /2))∼x−(x^2 /2) ⇒ f(x)∼((3x−((9x^2 )/2))/(x−(x^2 /2))) ⇒f(x)∼((3−((9x)/2))/(1−(x/2))) ⇒ lim_(x→0) f(x)=3
$${let}\:{f}\left({x}\right)=\frac{{ln}\left({sin}\left(\mathrm{3}{x}\right)+{cos}\left(\mathrm{3}{x}\right)\right)}{{ln}\left({sinx}+{cosx}\right)}\:\:{we}\:{have} \\ $$$${sin}\left(\mathrm{3}{x}\right)+{cos}\left(\mathrm{3}{x}\right)\sim\mathrm{3}{x}\:+\mathrm{1}−\frac{\left(\mathrm{3}{x}\right)^{\mathrm{2}} }{\mathrm{2}}\:=\mathrm{1}+\mathrm{3}{x}−\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${and}\:{ln}\left({sin}\left(\mathrm{3}{x}\right)+{cos}\left(\mathrm{3}{x}\right)\right)\sim{ln}\left(\mathrm{1}+\mathrm{3}{x}−\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$\sim\mathrm{3}{x}−\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${sin}\left({x}\right)+{cosx}\:\sim\:{x}+\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$${ln}\left(\:{sinx}\:+{cosx}\right)\sim\:{ln}\left(\mathrm{1}+{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\sim{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\frac{\mathrm{3}{x}−\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}}}{{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}\:\Rightarrow{f}\left({x}\right)\sim\frac{\mathrm{3}−\frac{\mathrm{9}{x}}{\mathrm{2}}}{\mathrm{1}−\frac{{x}}{\mathrm{2}}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\:{f}\left({x}\right)=\mathrm{3} \\ $$
Commented by M±th+et£s last updated on 13/Apr/20
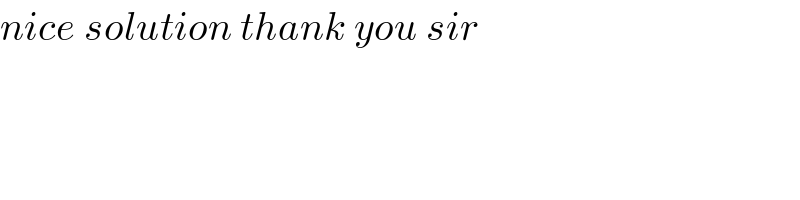
nice solution thank you sir
$${nice}\:{solution}\:{thank}\:{you}\:{sir} \\ $$$$ \\ $$
Answered by TANMAY PANACEA. last updated on 13/Apr/20
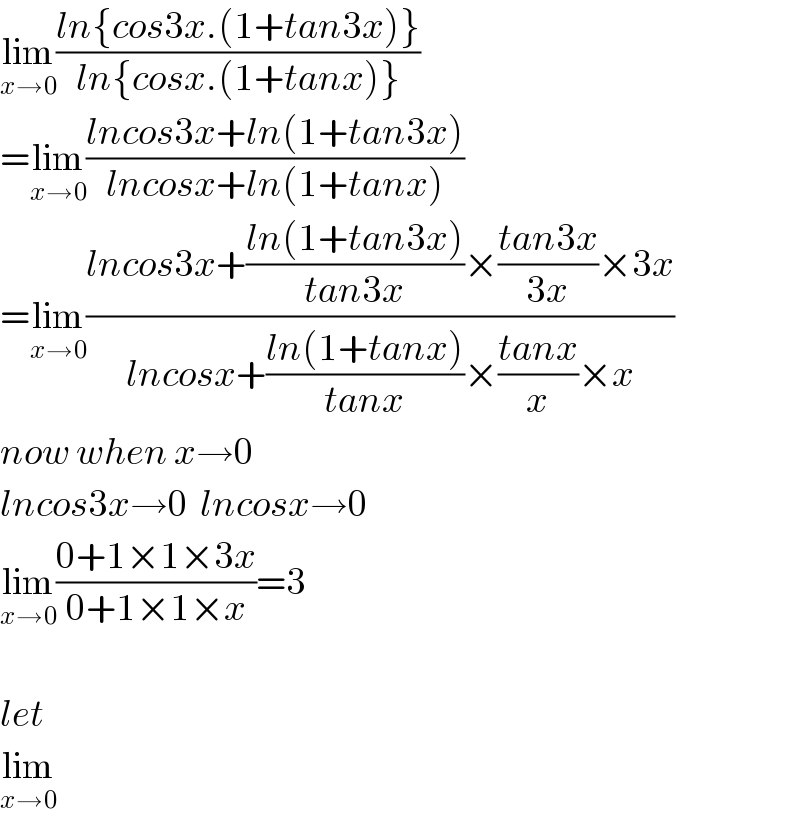
lim_(x→0) ((ln{cos3x.(1+tan3x)})/(ln{cosx.(1+tanx)})) =lim_(x→0) ((lncos3x+ln(1+tan3x))/(lncosx+ln(1+tanx))) =lim_(x→0) ((lncos3x+((ln(1+tan3x))/(tan3x))×((tan3x)/(3x))×3x)/(lncosx+((ln(1+tanx))/(tanx))×((tanx)/x)×x)) now when x→0 lncos3x→0 lncosx→0 lim_(x→0) ((0+1×1×3x)/(0+1×1×x))=3 let lim_(x→0)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{ln}\left\{{cos}\mathrm{3}{x}.\left(\mathrm{1}+{tan}\mathrm{3}{x}\right)\right\}}{{ln}\left\{{cosx}.\left(\mathrm{1}+{tanx}\right)\right\}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{lncos}\mathrm{3}{x}+{ln}\left(\mathrm{1}+{tan}\mathrm{3}{x}\right)}{{lncosx}+{ln}\left(\mathrm{1}+{tanx}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{lncos}\mathrm{3}{x}+\frac{{ln}\left(\mathrm{1}+{tan}\mathrm{3}{x}\right)}{{tan}\mathrm{3}{x}}×\frac{{tan}\mathrm{3}{x}}{\mathrm{3}{x}}×\mathrm{3}{x}}{{lncosx}+\frac{{ln}\left(\mathrm{1}+{tanx}\right)}{{tanx}}×\frac{{tanx}}{{x}}×{x}} \\ $$$${now}\:{when}\:{x}\rightarrow\mathrm{0} \\ $$$${lncos}\mathrm{3}{x}\rightarrow\mathrm{0}\:\:{lncosx}\rightarrow\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{0}+\mathrm{1}×\mathrm{1}×\mathrm{3}{x}}{\mathrm{0}+\mathrm{1}×\mathrm{1}×{x}}=\mathrm{3} \\ $$$$ \\ $$$${let} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}} \\ $$
Commented by M±th+et£s last updated on 13/Apr/20
nice work thank yoi very much sir
$${nice}\:{work}\:{thank}\:{yoi}\:{very}\:{much}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *