Question Number 85057 by kushdasbaghar@gmail.com last updated on 18/Mar/20
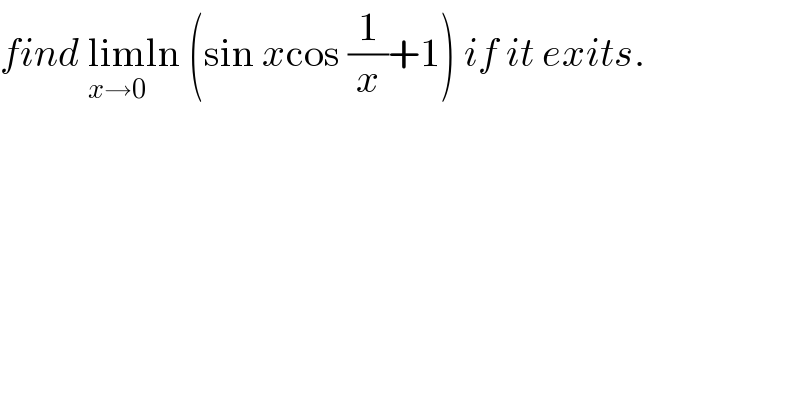
$${find}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}ln}\:\left(\mathrm{sin}\:{x}\mathrm{cos}\:\frac{\mathrm{1}}{{x}}+\mathrm{1}\right)\:{if}\:{it}\:{exits}. \\ $$
Commented by abdomathmax last updated on 19/Mar/20
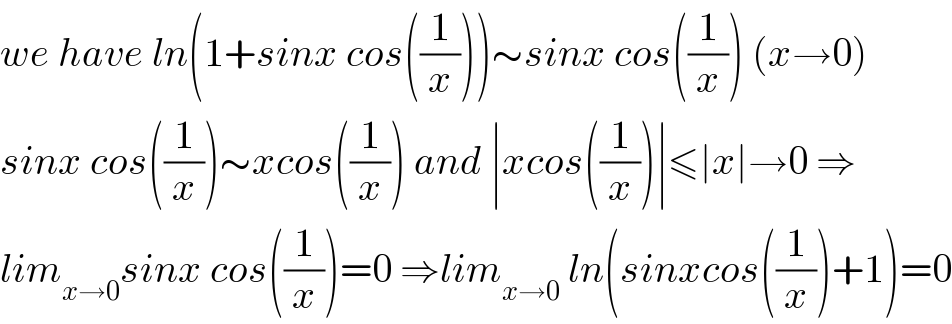
$${we}\:{have}\:{ln}\left(\mathrm{1}+{sinx}\:{cos}\left(\frac{\mathrm{1}}{{x}}\right)\right)\sim{sinx}\:{cos}\left(\frac{\mathrm{1}}{{x}}\right)\:\left({x}\rightarrow\mathrm{0}\right) \\ $$$${sinx}\:{cos}\left(\frac{\mathrm{1}}{{x}}\right)\sim{xcos}\left(\frac{\mathrm{1}}{{x}}\right)\:{and}\:\mid{xcos}\left(\frac{\mathrm{1}}{{x}}\right)\mid\leqslant\mid{x}\mid\rightarrow\mathrm{0}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} {sinx}\:{cos}\left(\frac{\mathrm{1}}{{x}}\right)=\mathrm{0}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:{ln}\left({sinxcos}\left(\frac{\mathrm{1}}{{x}}\right)+\mathrm{1}\right)=\mathrm{0} \\ $$
