Question Number 57404 by turbo msup by abdo last updated on 03/Apr/19
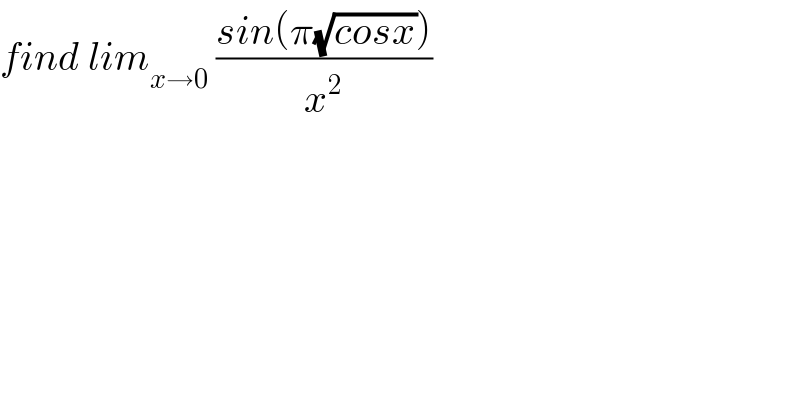
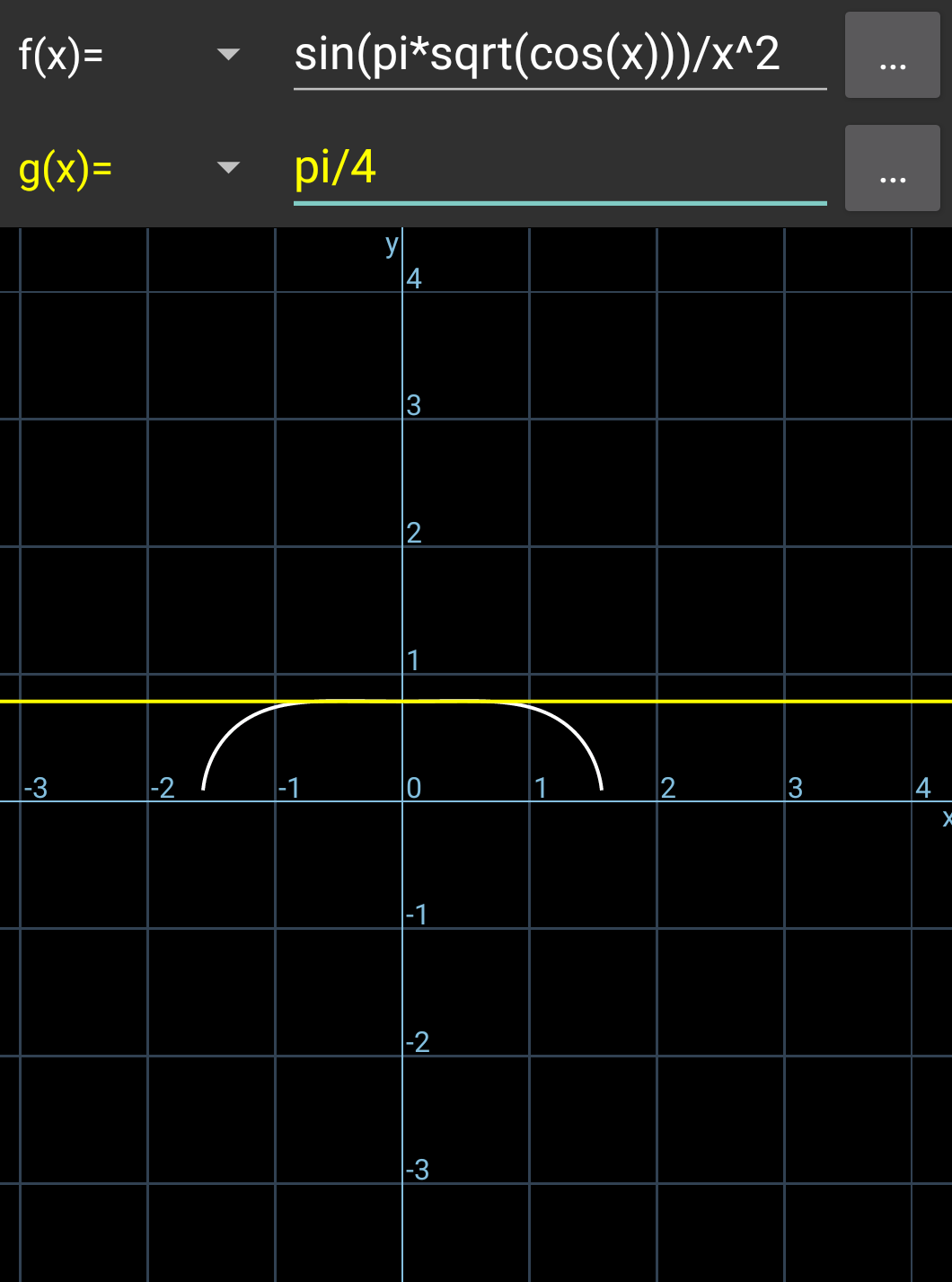
$${find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\frac{{sin}\left(\pi\sqrt{{cosx}}\right)}{{x}^{\mathrm{2}} } \\ $$
Commented by Smail last updated on 04/Apr/19
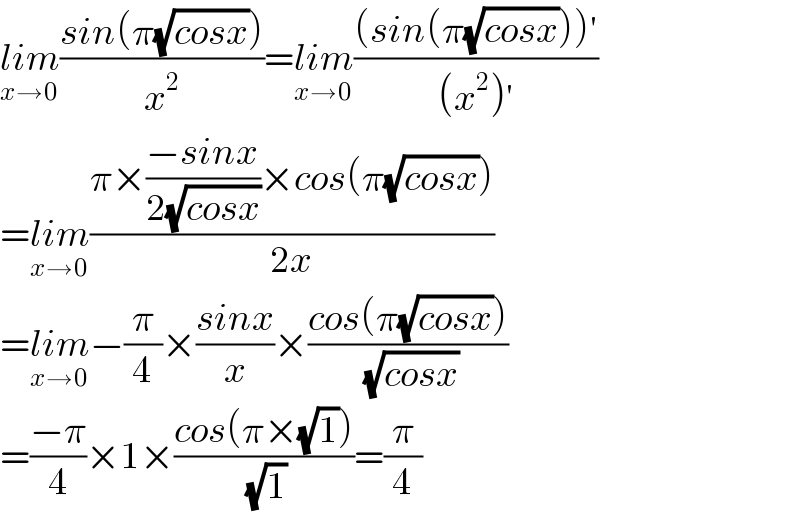
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{sin}\left(\pi\sqrt{{cosx}}\right)}{{x}^{\mathrm{2}} }=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\left({sin}\left(\pi\sqrt{{cosx}}\right)\right)'}{\left({x}^{\mathrm{2}} \right)'} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\pi×\frac{−{sinx}}{\mathrm{2}\sqrt{{cosx}}}×{cos}\left(\pi\sqrt{{cosx}}\right)}{\mathrm{2}{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}−\frac{\pi}{\mathrm{4}}×\frac{{sinx}}{{x}}×\frac{{cos}\left(\pi\sqrt{{cosx}}\right)}{\:\sqrt{{cosx}}} \\ $$$$=\frac{−\pi}{\mathrm{4}}×\mathrm{1}×\frac{{cos}\left(\pi×\sqrt{\mathrm{1}}\right)}{\:\sqrt{\mathrm{1}}}=\frac{\pi}{\mathrm{4}} \\ $$
Commented by maxmathsup by imad last updated on 04/Apr/19
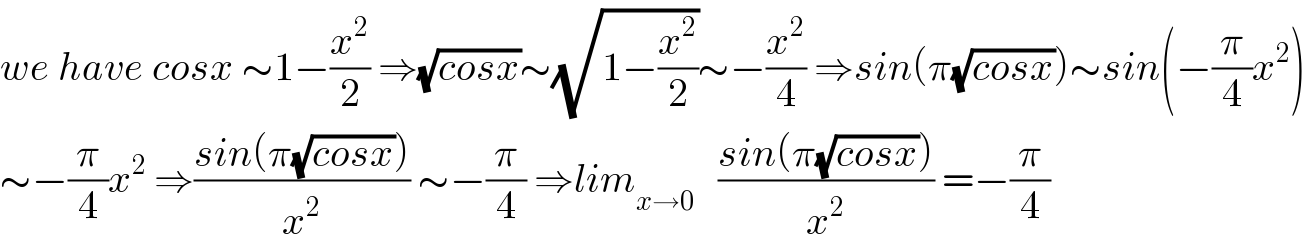
$${we}\:{have}\:{cosx}\:\sim\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\sqrt{{cosx}}\sim\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}\sim−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow{sin}\left(\pi\sqrt{{cosx}}\right)\sim{sin}\left(−\frac{\pi}{\mathrm{4}}{x}^{\mathrm{2}} \right) \\ $$$$\sim−\frac{\pi}{\mathrm{4}}{x}^{\mathrm{2}} \:\Rightarrow\frac{{sin}\left(\pi\sqrt{{cosx}}\right)}{{x}^{\mathrm{2}} }\:\sim−\frac{\pi}{\mathrm{4}}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{sin}\left(\pi\sqrt{{cosx}}\right)}{{x}^{\mathrm{2}} }\:=−\frac{\pi}{\mathrm{4}} \\ $$
Commented by Smail last updated on 04/Apr/19
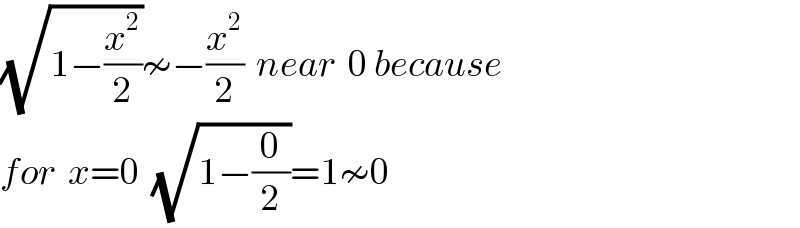
$$\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}\nsim−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\:{near}\:\:\mathrm{0}\:{because}\: \\ $$$${for}\:\:{x}=\mathrm{0}\:\:\sqrt{\mathrm{1}−\frac{\mathrm{0}}{\mathrm{2}}}=\mathrm{1}\nsim\mathrm{0} \\ $$
Commented by Smail last updated on 04/Apr/19
Commented by maxmathsup by imad last updated on 04/Apr/19
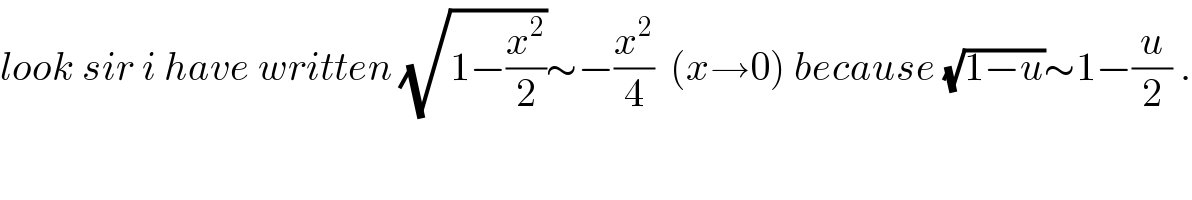
$${look}\:{sir}\:{i}\:{have}\:{written}\:\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}\sim−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:\:\left({x}\rightarrow\mathrm{0}\right)\:{because}\:\sqrt{\mathrm{1}−{u}}\sim\mathrm{1}−\frac{{u}}{\mathrm{2}}\:. \\ $$
Answered by kaivan.ahmadi last updated on 04/Apr/19
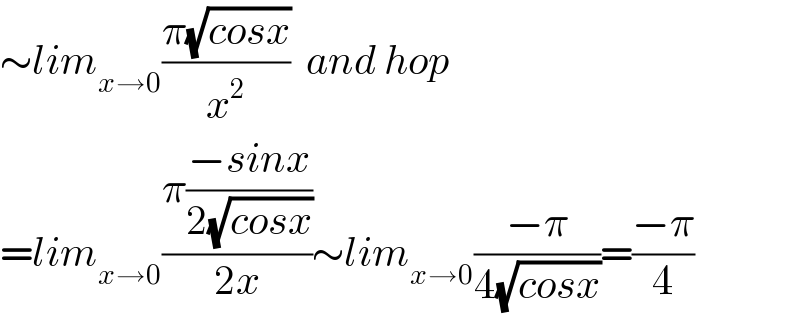
$$\sim{lim}_{{x}\rightarrow\mathrm{0}} \frac{\pi\sqrt{{cosx}}}{{x}^{\mathrm{2}} }\:\:{and}\:{hop} \\ $$$$={lim}_{{x}\rightarrow\mathrm{0}} \frac{\pi\frac{−{sinx}}{\mathrm{2}\sqrt{{cosx}}}}{\mathrm{2}{x}}\sim{lim}_{{x}\rightarrow\mathrm{0}} \frac{−\pi}{\mathrm{4}\sqrt{{cosx}}}=\frac{−\pi}{\mathrm{4}} \\ $$
