Question Number 162103 by HongKing last updated on 26/Dec/21
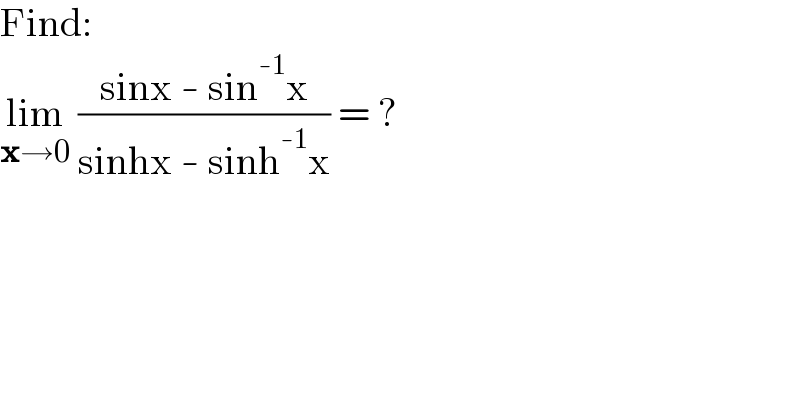
$$\mathrm{Find}: \\ $$$$\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sinx}\:-\:\mathrm{sin}^{-\mathrm{1}} \mathrm{x}}{\mathrm{sinhx}\:-\:\mathrm{sinh}^{-\mathrm{1}} \mathrm{x}}\:=\:? \\ $$
Answered by Ar Brandon last updated on 26/Dec/21
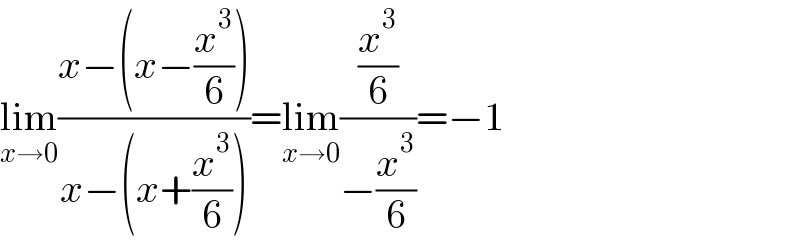
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)}{{x}−\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}{−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}=−\mathrm{1} \\ $$
Commented by HongKing last updated on 28/Dec/21
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{Sir} \\ $$
