Question Number 29845 by abdo imad last updated on 12/Feb/18
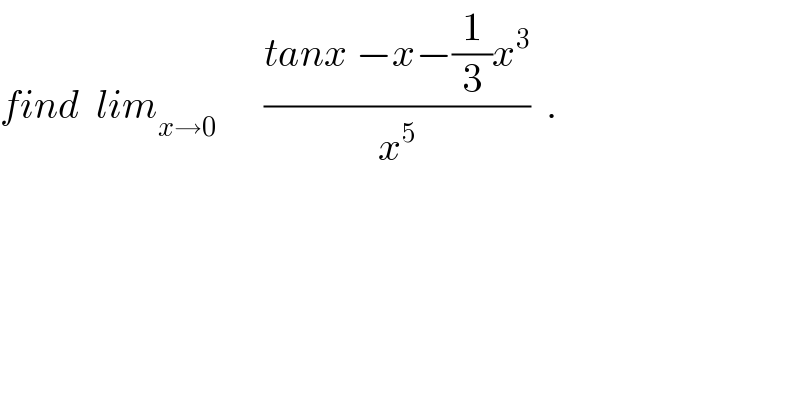
$${find}\:\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\:\:\frac{{tanx}\:−{x}−\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} }{{x}^{\mathrm{5}} }\:\:. \\ $$
Commented by Cheyboy last updated on 13/Feb/18
![lim_(x→0) ((sec^2 (x)−1−x^2 )/(5x^4 ))=(0/0) lim_(x→0) ((2(sec(x))sec(x)tan(x)−2x)/(20x^3 ))=(0/0) lim_(x→0) ((2(sec^2 (x)tan(x))−2x)/(20x^3 )) lim_(x→0) ((2[2(sec(x))sec(x)tan(x)]+sec^2 (x)sec^2 (x)−2)/(60x^2 )) lim_(x→0) ((2[2(sec^2 (x))tan(x)+sec^4 (x)]−2)/(60x^2 ))=(0/0) lim_(x→0) ((2[4(sec(x))sec(x)tan(x)+sec^4 (x)+4(sec^4 (x))tan(x)])/(120x))=(0/0) lim_(x→0) ((2[4(sec^2 (x)tan(x)+sec^4 (x)+4(sec^4 (x)tan(x)])/(120x)) lim_(x→0) ((2[8(sec^2 (x))tan^2 (x)+sec^4 (x)+4sec^4 (x)tan(x)+4(4sec^4 (x))tan^2 (x)+sec^6 (x)])/(120)) =((2(0)+2(1)+8(0)+4(0)+2(1))/(120)) =(4/(120))⇒(1/(30))](https://www.tinkutara.com/question/Q29858.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sec}^{\mathrm{2}} \left({x}\right)−\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{5}{x}^{\mathrm{4}} }=\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\left({sec}\left({x}\right)\right){sec}\left({x}\right){tan}\left({x}\right)−\mathrm{2}{x}}{\mathrm{20}{x}^{\mathrm{3}} }=\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\left({sec}^{\mathrm{2}} \left({x}\right){tan}\left({x}\right)\right)−\mathrm{2}{x}}{\mathrm{20}{x}^{\mathrm{3}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\left[\mathrm{2}\left({sec}\left({x}\right)\right){sec}\left({x}\right){tan}\left({x}\right)\right]+{sec}^{\mathrm{2}} \left({x}\right){sec}^{\mathrm{2}} \left({x}\right)−\mathrm{2}}{\mathrm{60}{x}^{\mathrm{2}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\left[\mathrm{2}\left({sec}^{\mathrm{2}} \left({x}\right)\right){tan}\left({x}\right)+{sec}^{\mathrm{4}} \left({x}\right)\right]−\mathrm{2}}{\mathrm{60}{x}^{\mathrm{2}} }=\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\left[\mathrm{4}\left({sec}\left({x}\right)\right){sec}\left({x}\right){tan}\left({x}\right)+{sec}^{\mathrm{4}} \left({x}\right)+\mathrm{4}\left({sec}^{\mathrm{4}} \left({x}\right)\right){tan}\left({x}\right)\right]}{\mathrm{120}{x}}=\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\left[\mathrm{4}\left({sec}^{\mathrm{2}} \left({x}\right){tan}\left({x}\right)+{sec}^{\mathrm{4}} \left({x}\right)+\mathrm{4}\left({sec}^{\mathrm{4}} \left({x}\right){tan}\left({x}\right)\right]\right.\right.}{\mathrm{120}{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\left[\mathrm{8}\left({sec}^{\mathrm{2}} \left({x}\right)\right){tan}^{\mathrm{2}} \left({x}\right)+{sec}^{\mathrm{4}} \left({x}\right)+\mathrm{4}{sec}^{\mathrm{4}} \left({x}\right){tan}\left({x}\right)+\mathrm{4}\left(\mathrm{4}{sec}^{\mathrm{4}} \left({x}\right)\right){tan}^{\mathrm{2}} \left({x}\right)+{sec}^{\mathrm{6}} \left({x}\right)\right]}{\mathrm{120}} \\ $$$$=\frac{\mathrm{2}\left(\mathrm{0}\right)+\mathrm{2}\left(\mathrm{1}\right)+\mathrm{8}\left(\mathrm{0}\right)+\mathrm{4}\left(\mathrm{0}\right)+\mathrm{2}\left(\mathrm{1}\right)}{\mathrm{120}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{120}}\Rightarrow\frac{\mathrm{1}}{\mathrm{30}} \\ $$
Commented by maxmathsup by imad last updated on 09/Apr/19
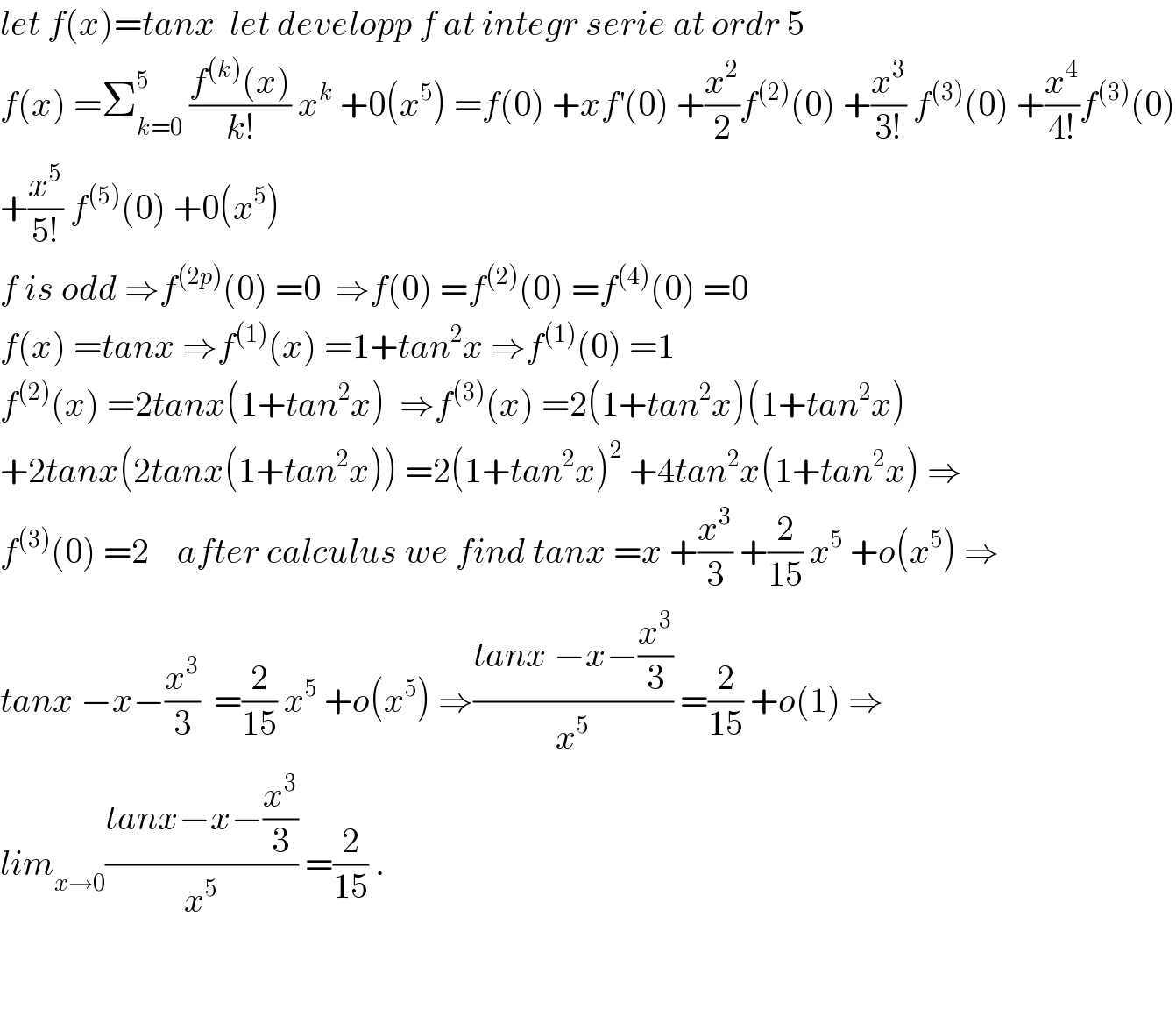
$${let}\:{f}\left({x}\right)={tanx}\:\:{let}\:{developp}\:{f}\:{at}\:{integr}\:{serie}\:{at}\:{ordr}\:\mathrm{5} \\ $$$${f}\left({x}\right)\:=\sum_{{k}=\mathrm{0}} ^{\mathrm{5}} \:\frac{{f}^{\left({k}\right)} \left({x}\right)}{{k}!}\:{x}^{{k}} \:+\mathrm{0}\left({x}^{\mathrm{5}} \right)\:={f}\left(\mathrm{0}\right)\:+{xf}^{'} \left(\mathrm{0}\right)\:+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{f}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\:+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}\:{f}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)\:+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}{f}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right) \\ $$$$+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}\:{f}^{\left(\mathrm{5}\right)} \left(\mathrm{0}\right)\:+\mathrm{0}\left({x}^{\mathrm{5}} \right) \\ $$$${f}\:{is}\:{odd}\:\Rightarrow{f}^{\left(\mathrm{2}{p}\right)} \left(\mathrm{0}\right)\:=\mathrm{0}\:\:\Rightarrow{f}\left(\mathrm{0}\right)\:={f}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\:={f}^{\left(\mathrm{4}\right)} \left(\mathrm{0}\right)\:=\mathrm{0} \\ $$$${f}\left({x}\right)\:={tanx}\:\Rightarrow{f}^{\left(\mathrm{1}\right)} \left({x}\right)\:=\mathrm{1}+{tan}^{\mathrm{2}} {x}\:\Rightarrow{f}^{\left(\mathrm{1}\right)} \left(\mathrm{0}\right)\:=\mathrm{1} \\ $$$${f}^{\left(\mathrm{2}\right)} \left({x}\right)\:=\mathrm{2}{tanx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\:\:\Rightarrow{f}^{\left(\mathrm{3}\right)} \left({x}\right)\:=\mathrm{2}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right) \\ $$$$+\mathrm{2}{tanx}\left(\mathrm{2}{tanx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\right)\:=\mathrm{2}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)^{\mathrm{2}} \:+\mathrm{4}{tan}^{\mathrm{2}} {x}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\:\Rightarrow \\ $$$${f}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)\:=\mathrm{2}\:\:\:\:{after}\:{calculus}\:{we}\:{find}\:{tanx}\:={x}\:+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:+\frac{\mathrm{2}}{\mathrm{15}}\:{x}^{\mathrm{5}} \:+{o}\left({x}^{\mathrm{5}} \right)\:\Rightarrow \\ $$$${tanx}\:−{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:\:=\frac{\mathrm{2}}{\mathrm{15}}\:{x}^{\mathrm{5}} \:+{o}\left({x}^{\mathrm{5}} \right)\:\Rightarrow\frac{{tanx}\:−{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}}{{x}^{\mathrm{5}} }\:=\frac{\mathrm{2}}{\mathrm{15}}\:+{o}\left(\mathrm{1}\right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \frac{{tanx}−{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}}{{x}^{\mathrm{5}} }\:=\frac{\mathrm{2}}{\mathrm{15}}\:. \\ $$$$ \\ $$$$ \\ $$
