Question Number 28429 by abdo imad last updated on 25/Jan/18
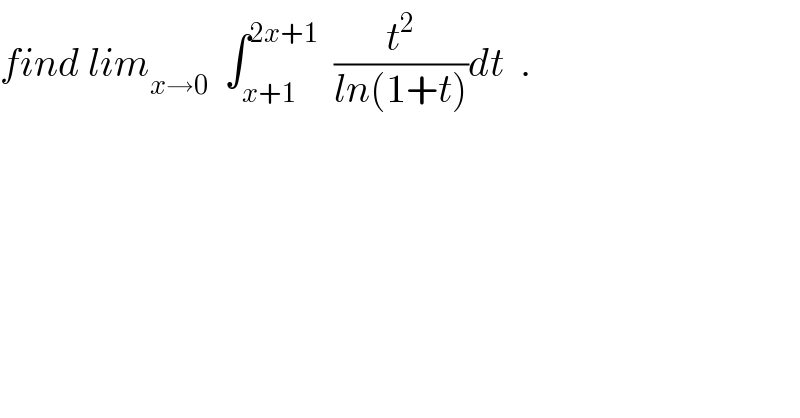
$${find}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\int_{{x}+\mathrm{1}} ^{\mathrm{2}{x}+\mathrm{1}} \:\:\frac{{t}^{\mathrm{2}} }{{ln}\left(\mathrm{1}+{t}\right)}{dt}\:\:. \\ $$
Commented by abdo imad last updated on 27/Jan/18
![∃ c ∈]x+1,2x+1[/ ∫_(x+1) ^(2x+1) = (1/(ln(1+c))) ∫_(x+1) ^(2x+1) t^2 dt = (1/3) (1/(ln(1+c))) ( (2x+1)^3 − (x+1)^3 ) we have x→0 ⇒ c→1 and lim_(x→0 ) ∫_(x+1) ^(2x+1) (t^2 /(ln(1+t)))dt =(1/(3ln2))×0=0 (look that the function w(t)= (1/(ln(1+t))) is continue on [x+1,2x+1] .)](https://www.tinkutara.com/question/Q28576.png)
$$\left.\exists\:{c}\:\in\right]{x}+\mathrm{1},\mathrm{2}{x}+\mathrm{1}\left[/\:\int_{{x}+\mathrm{1}} ^{\mathrm{2}{x}+\mathrm{1}} =\:\frac{\mathrm{1}}{{ln}\left(\mathrm{1}+{c}\right)}\:\int_{{x}+\mathrm{1}} ^{\mathrm{2}{x}+\mathrm{1}} \:{t}^{\mathrm{2}} {dt}\right. \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{3}}\:\frac{\mathrm{1}}{{ln}\left(\mathrm{1}+{c}\right)}\:\left(\:\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{3}} −\:\left({x}+\mathrm{1}\right)^{\mathrm{3}} \right)\:\:{we}\:{have}\:{x}\rightarrow\mathrm{0}\:\Rightarrow\:{c}\rightarrow\mathrm{1} \\ $$$${and}\:\:{lim}_{{x}\rightarrow\mathrm{0}\:} \:\int_{{x}+\mathrm{1}} ^{\mathrm{2}{x}+\mathrm{1}} \:\frac{{t}^{\mathrm{2}} }{{ln}\left(\mathrm{1}+{t}\right)}{dt}\:=\frac{\mathrm{1}}{\mathrm{3}{ln}\mathrm{2}}×\mathrm{0}=\mathrm{0} \\ $$$$\:\left({look}\:{that}\:{the}\:{function}\:{w}\left({t}\right)=\:\frac{\mathrm{1}}{{ln}\left(\mathrm{1}+{t}\right)}\:{is}\:{continue}\:{on}\right. \\ $$$$\left.\left[{x}+\mathrm{1},\mathrm{2}{x}+\mathrm{1}\right]\:.\right) \\ $$$$ \\ $$
