Question Number 32990 by abdo imad last updated on 09/Apr/18
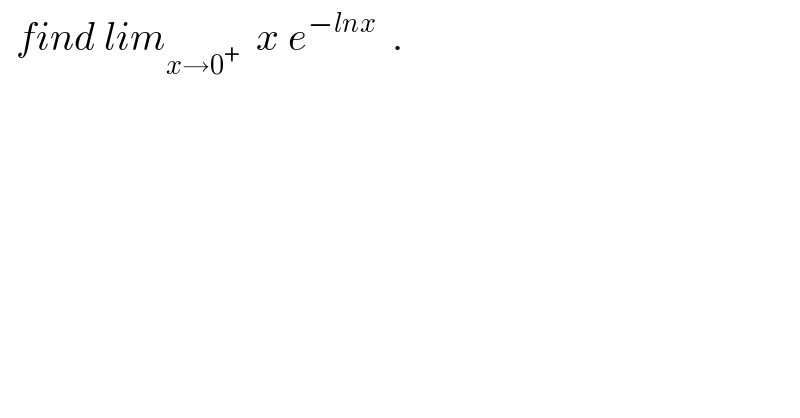
$$\:\:{find}\:{lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:{x}\:{e}^{−{lnx}} \:\:. \\ $$
Commented by prof Abdo imad last updated on 09/Apr/18
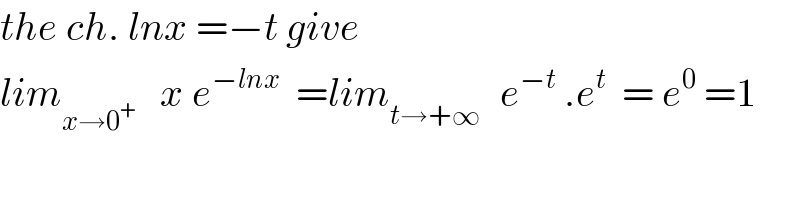
$${the}\:{ch}.\:{lnx}\:=−{t}\:{give} \\ $$$${lim}_{{x}\rightarrow\mathrm{0}^{+} } \:\:\:{x}\:{e}^{−{lnx}} \:\:={lim}_{{t}\rightarrow+\infty\:} \:\:{e}^{−{t}} \:.{e}^{{t}} \:\:=\:{e}^{\mathrm{0}} \:=\mathrm{1} \\ $$
Answered by kyle_TW last updated on 09/Apr/18
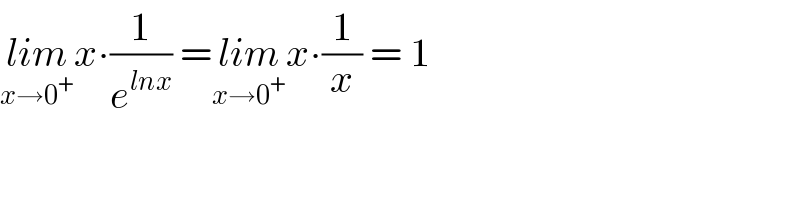
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {{lim}x}\centerdot\frac{\mathrm{1}}{{e}^{{lnx}} }\:=\underset{{x}\rightarrow\mathrm{0}^{+} } {{lim}x}\centerdot\frac{\mathrm{1}}{{x}}\:=\:\mathrm{1} \\ $$
