Question Number 57410 by Abdo msup. last updated on 03/Apr/19
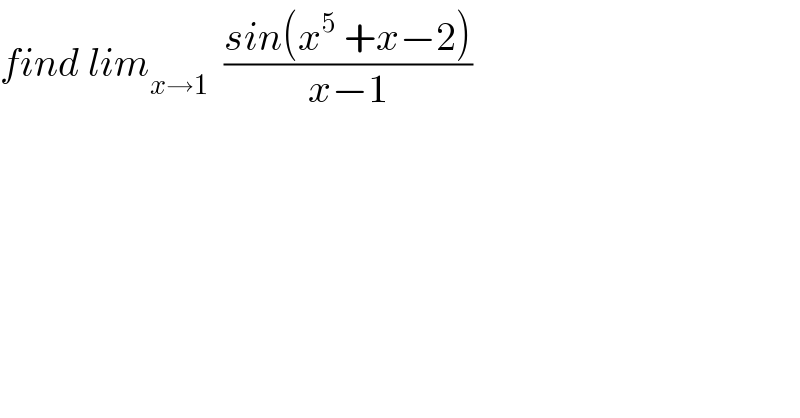
$${find}\:{lim}_{{x}\rightarrow\mathrm{1}} \:\:\frac{{sin}\left({x}^{\mathrm{5}} \:+{x}−\mathrm{2}\right)}{{x}−\mathrm{1}} \\ $$
Commented by maxmathsup by imad last updated on 04/Apr/19
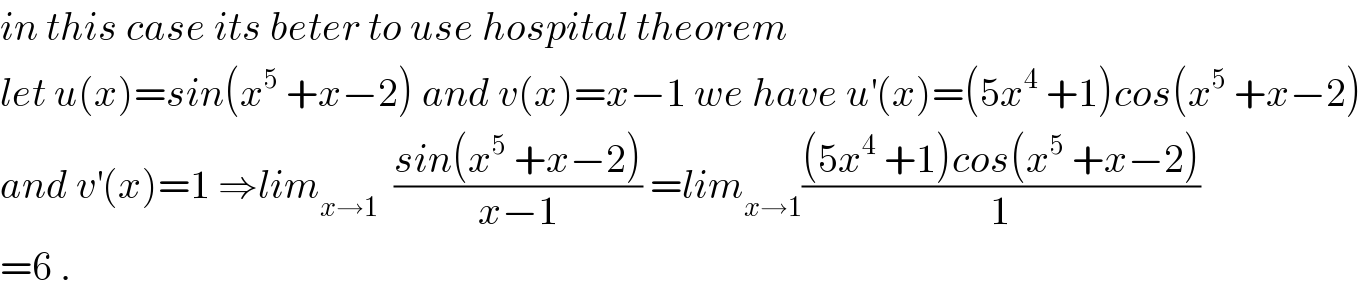
$${in}\:{this}\:{case}\:{its}\:{beter}\:{to}\:{use}\:{hospital}\:{theorem} \\ $$$${let}\:{u}\left({x}\right)={sin}\left({x}^{\mathrm{5}} \:+{x}−\mathrm{2}\right)\:{and}\:{v}\left({x}\right)={x}−\mathrm{1}\:{we}\:{have}\:{u}^{'} \left({x}\right)=\left(\mathrm{5}{x}^{\mathrm{4}} \:+\mathrm{1}\right){cos}\left({x}^{\mathrm{5}} \:+{x}−\mathrm{2}\right) \\ $$$${and}\:{v}^{'} \left({x}\right)=\mathrm{1}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{1}} \:\:\frac{{sin}\left({x}^{\mathrm{5}} \:+{x}−\mathrm{2}\right)}{{x}−\mathrm{1}}\:={lim}_{{x}\rightarrow\mathrm{1}} \frac{\left(\mathrm{5}{x}^{\mathrm{4}} \:+\mathrm{1}\right){cos}\left({x}^{\mathrm{5}} \:+{x}−\mathrm{2}\right)}{\mathrm{1}} \\ $$$$=\mathrm{6}\:. \\ $$
Answered by kaivan.ahmadi last updated on 03/Apr/19
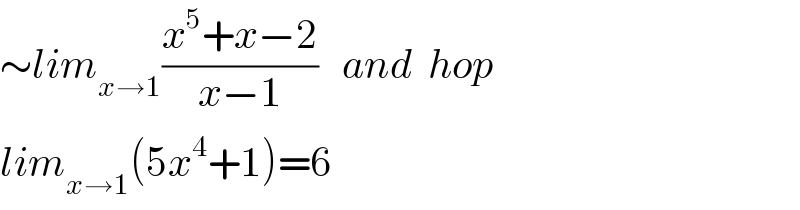
$$\sim{lim}_{{x}\rightarrow\mathrm{1}} \frac{{x}^{\mathrm{5}} +{x}−\mathrm{2}}{{x}−\mathrm{1}}\:\:\:{and}\:\:{hop} \\ $$$${lim}_{{x}\rightarrow\mathrm{1}} \left(\mathrm{5}{x}^{\mathrm{4}} +\mathrm{1}\right)=\mathrm{6} \\ $$
