Question Number 155620 by mathdanisur last updated on 02/Oct/21
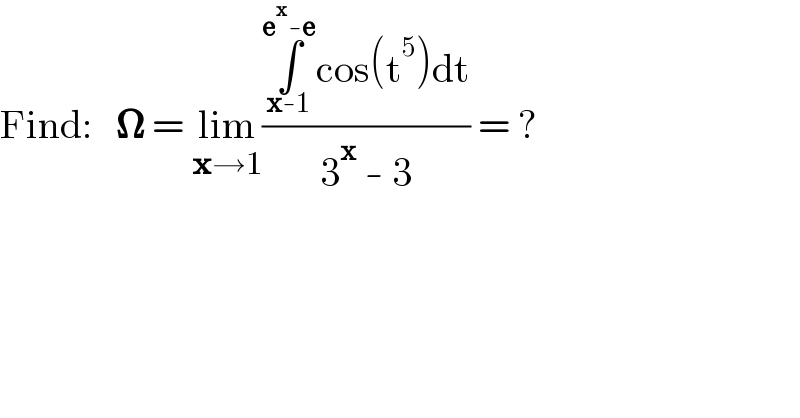
$$\mathrm{Find}:\:\:\:\boldsymbol{\Omega}\:=\:\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\underset{\boldsymbol{\mathrm{x}}-\mathrm{1}} {\overset{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} -\boldsymbol{\mathrm{e}}} {\int}}\mathrm{cos}\left(\mathrm{t}^{\mathrm{5}} \right)\mathrm{dt}}{\mathrm{3}^{\boldsymbol{\mathrm{x}}} \:-\:\mathrm{3}}\:=\:? \\ $$
Answered by mindispower last updated on 04/Oct/21
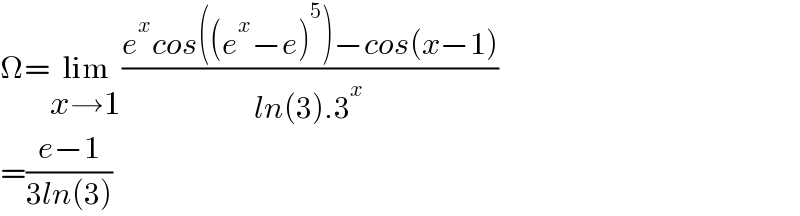
$$\Omega=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{e}^{{x}} {cos}\left(\left({e}^{{x}} −{e}\right)^{\mathrm{5}} \right)−{cos}\left({x}−\mathrm{1}\right)}{{ln}\left(\mathrm{3}\right).\mathrm{3}^{{x}} } \\ $$$$=\frac{{e}−\mathrm{1}}{\mathrm{3}{ln}\left(\mathrm{3}\right)} \\ $$
