Question Number 29157 by abdo imad last updated on 04/Feb/18
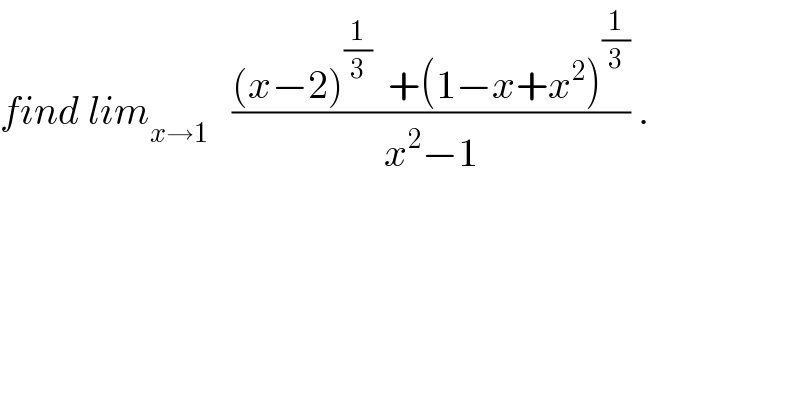
$${find}\:{lim}_{{x}\rightarrow\mathrm{1}} \:\:\:\frac{\left({x}−\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\:+\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{{x}^{\mathrm{2}} −\mathrm{1}}\:. \\ $$
Commented by abdo imad last updated on 07/Feb/18

$${let}\:{use}\:{hospital}\:{theorem} \\ $$$${lim}_{{x}\rightarrow\mathrm{1}} \left(…\right)={lim}_{{x}\rightarrow\mathrm{1}} \:\:\:\:\:\frac{\frac{\mathrm{1}}{\mathrm{3}}\left({x}−\mathrm{2}\right)^{\frac{−\mathrm{2}}{\mathrm{3}}} \:+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}{x}−\mathrm{1}\right)^{−\frac{\mathrm{2}}{\mathrm{3}}} }{\mathrm{2}{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\:\left(−\mathrm{1}\right)^{−\frac{\mathrm{2}}{\mathrm{3}}} \:\:+\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\:\left(\:\left(−\mathrm{1}\right)^{−\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:+\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\:\frac{\mathrm{4}}{\mathrm{3}}\right)=\:\frac{\mathrm{2}}{\mathrm{3}}. \\ $$
Answered by iv@0uja last updated on 07/Feb/18
![let a=(x−2)^(1/3) ,b=(1−x+x^2 )^(1/3) (((x−2)^(1/3) +(1−x+x^(1/3) ))/(x^2 −1)) =((a+b)/(x^2 −1)) =(((a+b)(a^2 −ab+b^2 ))/((x^2 −1)(a^2 −ab+b^2 ))) =((a^3 +b^3 )/((x^2 −1)(a^2 −ab+b^2 ))) =(((x−2)+(1−x+x^2 ))/((x^2 −1)(a^2 −ab+b^2 ))) =(1/(a^2 −ab+b^2 )) =(1/((x−2)^(2/3) +(x−2)^(1/3) (1−x+x^2 )^(1/3) +(1−x+x^2 )^(2/3) )) lim_(x→1) (((x−2)^(1/3) +(1−x+x^2 )^(1/3) )/(x^2 −1)) =lim_(x→1) (1/((x−2)^(2/3) +{(x−2)(1−x+x^2 )}^(1/3) +(1−x+x^2 )^(2/3) )) =lim_(x→1) (1/((−1)^(2/3) +(−1∙1)^(1/3) +1^(2/3) )) =(1/((−1)^2 +(−1)+1))=1 [(−1)^(1/3) =((−1))^(1/3) =−1]](https://www.tinkutara.com/question/Q29255.png)
$$\mathrm{let}\:{a}=\left({x}−\mathrm{2}\right)^{\mathrm{1}/\mathrm{3}} ,{b}=\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)^{\mathrm{1}/\mathrm{3}} \\ $$$$\:\:\:\:\frac{\left({x}−\mathrm{2}\right)^{\mathrm{1}/\mathrm{3}} +\left(\mathrm{1}−{x}+{x}^{\mathrm{1}/\mathrm{3}} \right)}{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\frac{{a}+{b}}{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\frac{\left({a}+{b}\right)\left({a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \right)} \\ $$$$=\frac{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} }{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \right)} \\ $$$$=\frac{\left({x}−\mathrm{2}\right)+\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{{a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}/\mathrm{3}} +\left({x}−\mathrm{2}\right)^{\mathrm{1}/\mathrm{3}} \left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)^{\mathrm{1}/\mathrm{3}} +\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)^{\mathrm{2}/\mathrm{3}} } \\ $$$$\:\:\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left({x}−\mathrm{2}\right)^{\mathrm{1}/\mathrm{3}} +\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)^{\mathrm{1}/\mathrm{3}} }{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}/\mathrm{3}} +\left\{\left({x}−\mathrm{2}\right)\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)\right\}^{\mathrm{1}/\mathrm{3}} +\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)^{\mathrm{2}/\mathrm{3}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}}{\left(−\mathrm{1}\right)^{\mathrm{2}/\mathrm{3}} +\left(−\mathrm{1}\centerdot\mathrm{1}\right)^{\mathrm{1}/\mathrm{3}} +\mathrm{1}^{\mathrm{2}/\mathrm{3}} } \\ $$$$=\frac{\mathrm{1}}{\left(−\mathrm{1}\right)^{\mathrm{2}} +\left(−\mathrm{1}\right)+\mathrm{1}}=\mathrm{1} \\ $$$$\left[\left(−\mathrm{1}\right)^{\mathrm{1}/\mathrm{3}} =\sqrt[{\mathrm{3}}]{−\mathrm{1}}=−\mathrm{1}\right] \\ $$
