Question Number 97990 by abdomathmax last updated on 10/Jun/20
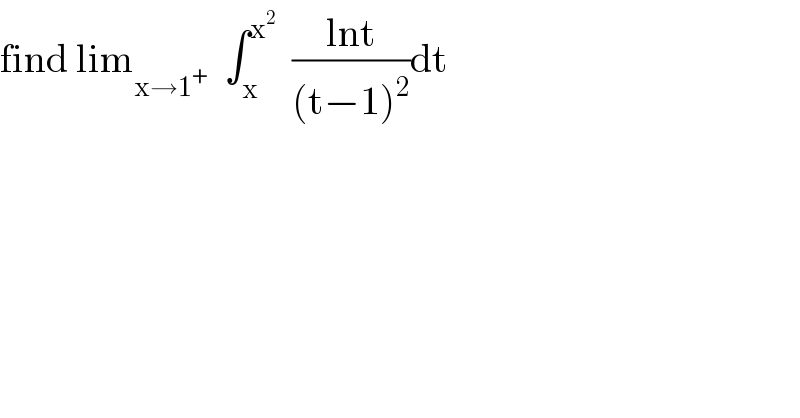
$$\mathrm{find}\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}^{+} } \:\:\int_{\mathrm{x}} ^{\mathrm{x}^{\mathrm{2}} } \:\:\frac{\mathrm{lnt}}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$
Answered by maths mind last updated on 11/Jun/20
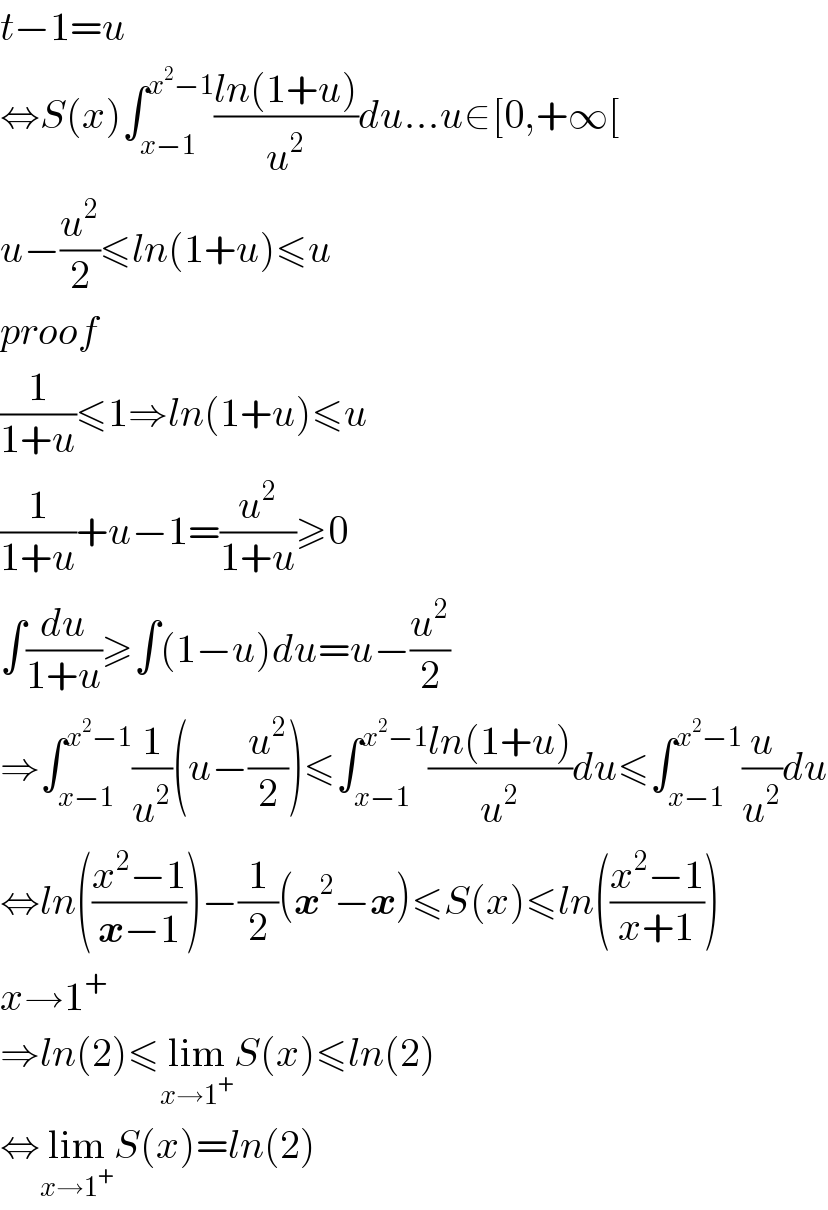
$${t}−\mathrm{1}={u} \\ $$$$\Leftrightarrow{S}\left({x}\right)\int_{{x}−\mathrm{1}} ^{{x}^{\mathrm{2}} −\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{u}\right)}{{u}^{\mathrm{2}} }{du}…{u}\in\left[\mathrm{0},+\infty\left[\right.\right. \\ $$$${u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\leqslant{ln}\left(\mathrm{1}+{u}\right)\leqslant{u} \\ $$$${proof}\:\:\: \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{u}}\leqslant\mathrm{1}\Rightarrow{ln}\left(\mathrm{1}+{u}\right)\leqslant{u} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{u}}+{u}−\mathrm{1}=\frac{{u}^{\mathrm{2}} }{\mathrm{1}+{u}}\geqslant\mathrm{0} \\ $$$$\int\frac{{du}}{\mathrm{1}+{u}}\geqslant\int\left(\mathrm{1}−{u}\right){du}={u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\int_{{x}−\mathrm{1}} ^{{x}^{\mathrm{2}} −\mathrm{1}} \frac{\mathrm{1}}{{u}^{\mathrm{2}} }\left({u}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\right)\leqslant\int_{{x}−\mathrm{1}} ^{{x}^{\mathrm{2}} −\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{u}\right)}{{u}^{\mathrm{2}} }{du}\leqslant\int_{{x}−\mathrm{1}} ^{{x}^{\mathrm{2}} −\mathrm{1}} \frac{{u}}{{u}^{\mathrm{2}} }{du} \\ $$$$\Leftrightarrow{ln}\left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\boldsymbol{{x}}−\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\boldsymbol{{x}}^{\mathrm{2}} −\boldsymbol{{x}}\right)\leqslant{S}\left({x}\right)\leqslant{ln}\left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}+\mathrm{1}}\right) \\ $$$${x}\rightarrow\mathrm{1}^{+} \\ $$$$\Rightarrow{ln}\left(\mathrm{2}\right)\leqslant\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}{S}\left({x}\right)\leqslant{ln}\left(\mathrm{2}\right) \\ $$$$\Leftrightarrow\underset{{x}\rightarrow\mathrm{1}^{+} } {\mathrm{lim}}{S}\left({x}\right)={ln}\left(\mathrm{2}\right) \\ $$
Commented by mathmax by abdo last updated on 12/Jun/20

$$\mathrm{thankx}\:\mathrm{sir}. \\ $$
