Find-lim-x-2-1-x-1-pi-x-x-3-8-

Question Number 160444 by HongKing last updated on 29/Nov/21

Find : \lim_{x \to 2} \frac{Γ (\frac{1}{x} + 1) - \frac{\sqrt{π}}{x}}{x^{3} - 8} = ?

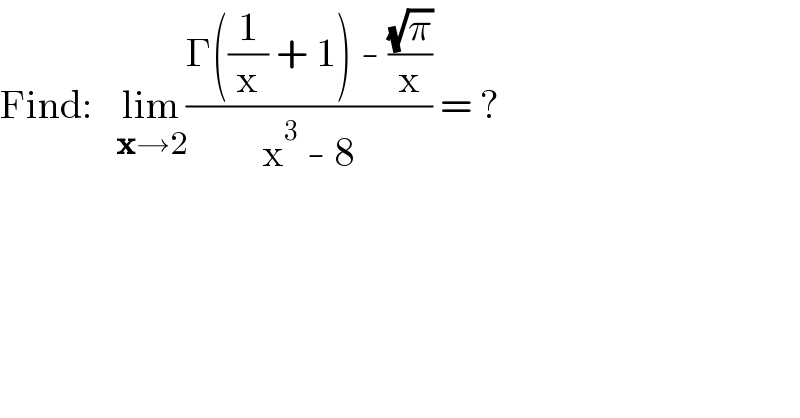
Answered by Ar Brandon last updated on 29/Nov/21

L = \lim_{x \to 2} \frac{Γ (\frac{1}{x} + 1) - \frac{\sqrt{π}}{x}}{x^{3} - 8}

= \lim_{x \to 2} \frac{- \frac{1}{x^{2}} Γ (\frac{1}{x} + 1) ψ (\frac{1}{x} + 1) + \frac{\sqrt{π}}{x^{2}}}{3 x^{2}}

= \frac{1}{12} (\frac{\sqrt{π}}{4} - \frac{1}{4} Γ (\frac{3}{2}) ψ (\frac{3}{2}))

= \frac{1}{12} (\frac{\sqrt{π}}{4} - \frac{\sqrt{π}}{8} (2 - γ - 2 \ln 2))

= \frac{\sqrt{π}}{96} (γ + 2 \ln 2)

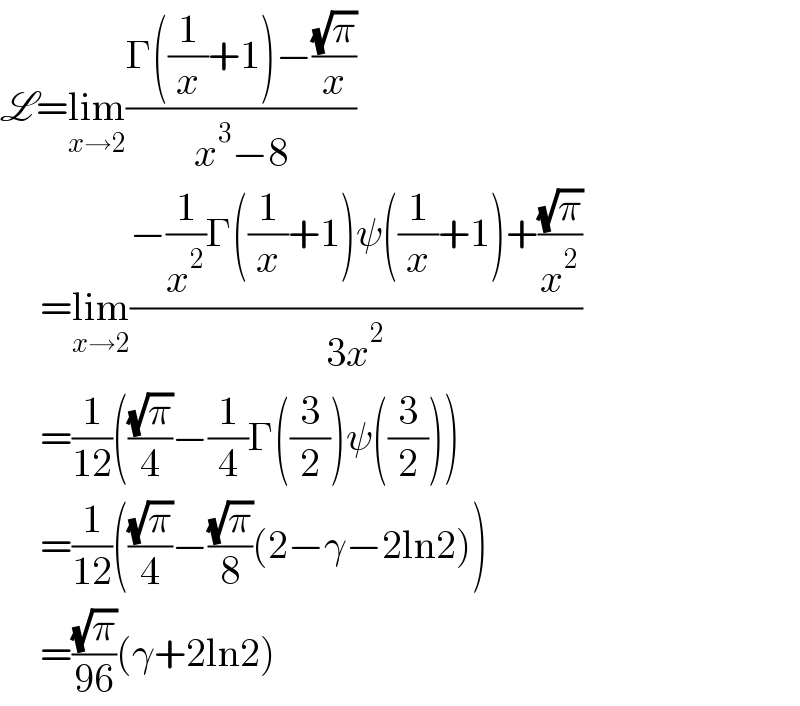
Commented by HongKing last updated on 29/Nov/21

perfect my dear Sir thank you so much

Answered by mnjuly1970 last updated on 30/Nov/21

- - - - - - - -

s o l u t i o n

L : \underset{rule}{\overset{{Hopital}^{'} s}{=}} {l i m}_{x \to 2} \frac{\frac{- 1}{x^{2}} Γ^{'} (1 + \frac{1}{x}) + \frac{\sqrt{π}}{x^{2}}}{3 x^{2}}

:= {l i m}_{x \to 2} \frac{\sqrt{π} - Γ^{'} (1 + \frac{1}{x})}{3 x^{4}}

∴ L := \frac{\sqrt{π} - Γ^{'} (\frac{3}{2})}{48} = \frac{\sqrt{π} - ψ (\frac{3}{2}) Γ (\frac{3}{2})}{48}

= \frac{\sqrt{π} - \frac{1}{2} (2 - γ - l n (4)) . \sqrt{π}}{48}

L := \frac{\sqrt{π} (γ + l n (4)}{96}

Commented by HongKing last updated on 30/Nov/21

perfect my dear Ser thank you so much

Commented by mnjuly1970 last updated on 01/Dec/21

t h a n k y o u s o m u c h f o r y o u r

n i c e q u e s t i o n s . . s i r H o n g K i n g

Commented by HongKing last updated on 01/Dec/21

thank you my dear Sir