Question Number 189757 by Shrinava last updated on 21/Mar/23
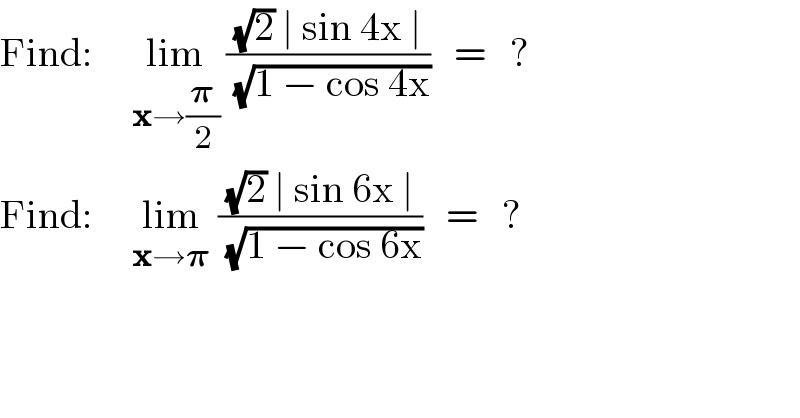
$$\mathrm{Find}:\:\:\:\:\:\underset{\boldsymbol{\mathrm{x}}\rightarrow\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}}\:\mid\:\mathrm{sin}\:\mathrm{4x}\:\mid}{\:\sqrt{\mathrm{1}\:−\:\mathrm{cos}\:\mathrm{4x}}}\:\:\:=\:\:\:? \\ $$$$\mathrm{Find}:\:\:\:\:\:\underset{\boldsymbol{\mathrm{x}}\rightarrow\boldsymbol{\pi}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{2}}\:\mid\:\mathrm{sin}\:\mathrm{6x}\:\mid}{\:\sqrt{\mathrm{1}\:−\:\mathrm{cos}\:\mathrm{6x}}}\:\:\:=\:\:\:? \\ $$
Answered by Frix last updated on 21/Mar/23
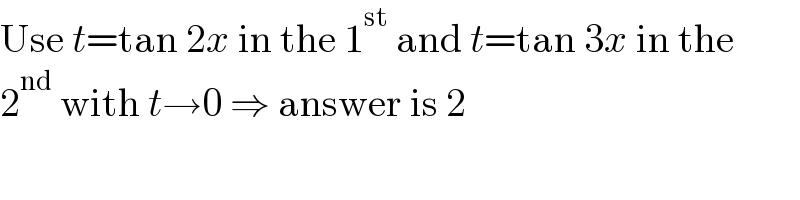
$$\mathrm{Use}\:{t}=\mathrm{tan}\:\mathrm{2}{x}\:\mathrm{in}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{and}\:{t}=\mathrm{tan}\:\mathrm{3}{x}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{2}^{\mathrm{nd}} \:\mathrm{with}\:{t}\rightarrow\mathrm{0}\:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{2} \\ $$
Answered by mehdee42 last updated on 21/Mar/23
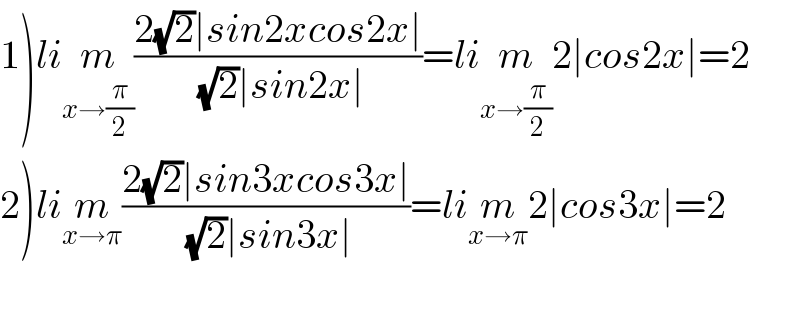
$$\left.\mathrm{1}\right){li}\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {{m}}\frac{\mathrm{2}\sqrt{\mathrm{2}}\mid{sin}\mathrm{2}{xcos}\mathrm{2}{x}\mid}{\:\sqrt{\mathrm{2}}\mid{sin}\mathrm{2}{x}\mid}={li}\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {{m}}\mathrm{2}\mid{cos}\mathrm{2}{x}\mid=\mathrm{2} \\ $$$$\left.\mathrm{2}\right){li}\underset{{x}\rightarrow\pi} {{m}}\frac{\mathrm{2}\sqrt{\mathrm{2}}\mid{sin}\mathrm{3}{xcos}\mathrm{3}{x}\mid}{\:\sqrt{\mathrm{2}}\mid{sin}\mathrm{3}{x}\mid}={li}\underset{{x}\rightarrow\pi} {{m}}\mathrm{2}\mid{cos}\mathrm{3}{x}\mid=\mathrm{2} \\ $$$$ \\ $$
Commented by Shrinava last updated on 24/Mar/23
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{professor} \\ $$
