Question Number 160282 by HongKing last updated on 27/Nov/21

$$\mathrm{Find}:\:\:\:\:\:\underset{\boldsymbol{\mathrm{x}}\rightarrow\boldsymbol{\mathrm{b}}} {\mathrm{lim}}\:\frac{\mathrm{b}^{\boldsymbol{\mathrm{x}}} \:-\:\mathrm{x}^{\boldsymbol{\mathrm{b}}} }{\mathrm{x}\:-\:\mathrm{b}} \\ $$
Answered by puissant last updated on 27/Nov/21
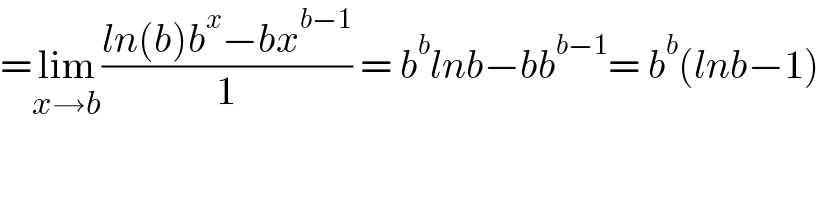
$$=\underset{{x}\rightarrow{b}} {\mathrm{lim}}\frac{{ln}\left({b}\right){b}^{{x}} −{bx}^{{b}−\mathrm{1}} }{\mathrm{1}}\:=\:{b}^{{b}} {lnb}−{bb}^{{b}−\mathrm{1}} =\:{b}^{{b}} \left({lnb}−\mathrm{1}\right) \\ $$
