Question Number 148326 by Odhiambojr last updated on 27/Jul/21
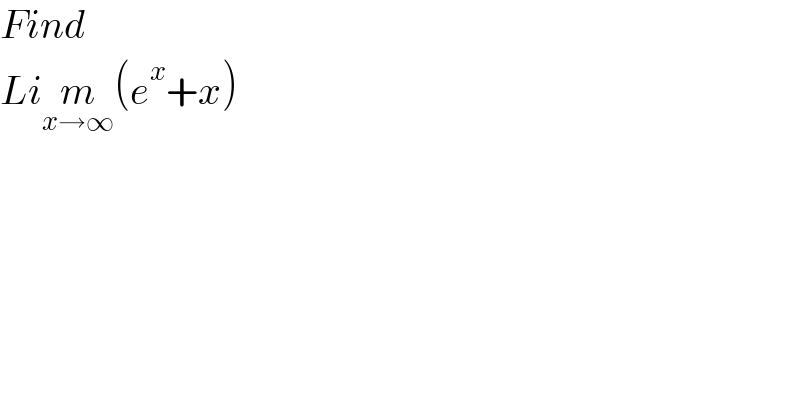
$${Find}\: \\ $$$${Li}\underset{{x}\rightarrow\infty} {{m}}\left({e}^{{x}} +{x}\right) \\ $$
Answered by mathmax by abdo last updated on 27/Jul/21
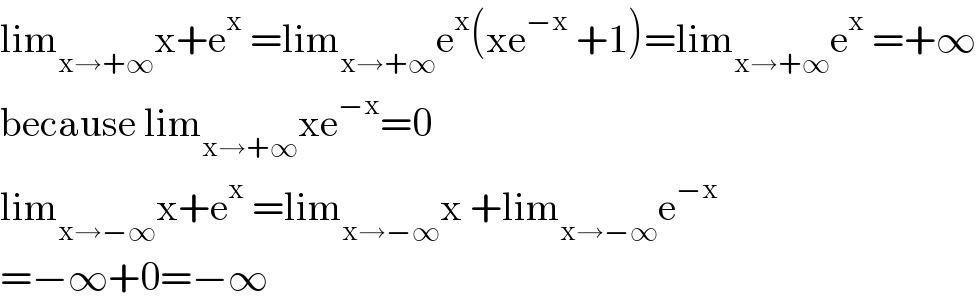
$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{x}+\mathrm{e}^{\mathrm{x}} \:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{e}^{\mathrm{x}} \left(\mathrm{xe}^{−\mathrm{x}} \:+\mathrm{1}\right)=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{e}^{\mathrm{x}} \:=+\infty \\ $$$$\mathrm{because}\:\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{xe}^{−\mathrm{x}} =\mathrm{0} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} \mathrm{x}+\mathrm{e}^{\mathrm{x}} \:=\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} \mathrm{x}\:+\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} \mathrm{e}^{−\mathrm{x}} \\ $$$$=−\infty+\mathrm{0}=−\infty \\ $$
