Question Number 27789 by abdo imad last updated on 14/Jan/18
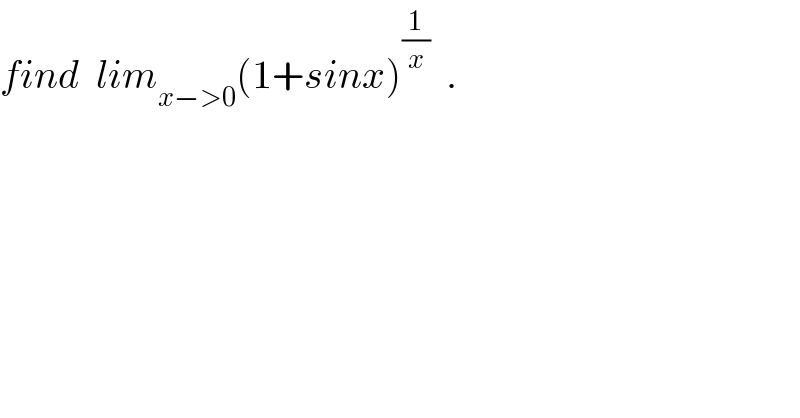
$${find}\:\:{lim}_{{x}−>\mathrm{0}} \left(\mathrm{1}+{sinx}\right)^{\frac{\mathrm{1}}{{x}}} \:\:. \\ $$
Commented by abdo imad last updated on 15/Jan/18
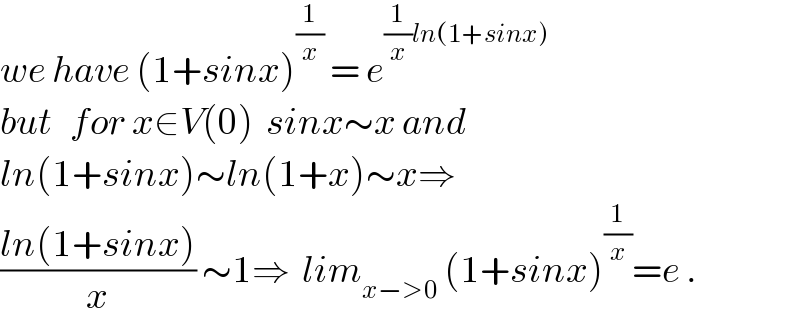
$${we}\:{have}\:\left(\mathrm{1}+{sinx}\right)^{\frac{\mathrm{1}}{{x}}} \:=\:{e}^{\frac{\mathrm{1}}{{x}}{ln}\left(\mathrm{1}+{sinx}\right)} \\ $$$${but}\:\:\:{for}\:{x}\in{V}\left(\mathrm{0}\right)\:\:{sinx}\sim{x}\:{and} \\ $$$${ln}\left(\mathrm{1}+{sinx}\right)\sim{ln}\left(\mathrm{1}+{x}\right)\sim{x}\Rightarrow \\ $$$$\frac{{ln}\left(\mathrm{1}+{sinx}\right)}{{x}}\:\sim\mathrm{1}\Rightarrow\:\:{lim}_{{x}−>\mathrm{0}} \:\left(\mathrm{1}+{sinx}\right)^{\frac{\mathrm{1}}{{x}}} ={e}\:. \\ $$
Commented by prakash jain last updated on 16/Jan/18

$$\mathrm{thanks}.\:\mathrm{your}\:\mathrm{question}\:\mathrm{and}\:\mathrm{solution} \\ $$$$\mathrm{are}\:\mathrm{great}\:\mathrm{learning}\:\mathrm{experience} \\ $$
Commented by abdo imad last updated on 16/Jan/18
$${thsnk}\:{you}\:{friend}\:\:{prakash}… \\ $$
