Question Number 27786 by abdo imad last updated on 14/Jan/18
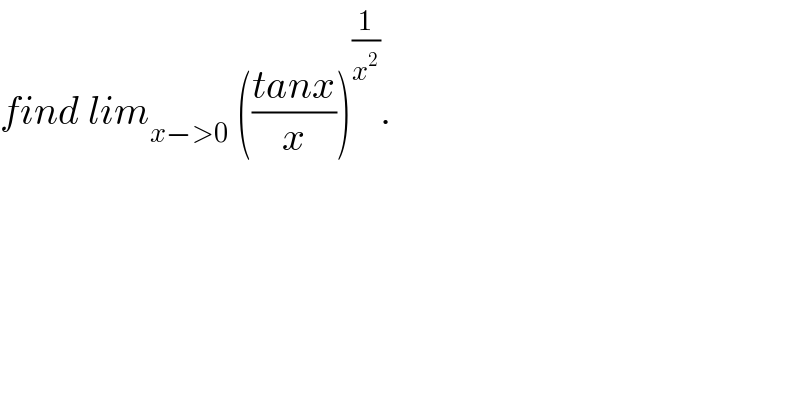
$${find}\:{lim}_{{x}−>\mathrm{0}} \:\left(\frac{{tanx}}{{x}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} . \\ $$
Commented by abdo imad last updated on 17/Jan/18

$${we}\:{have}\:\:\left(\frac{{tanx}}{{x}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} =\:\:{e}^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:{ln}\left(\frac{{tanx}}{{x}}\right)} {but}\:{we}\:{have} \\ $$$${tanx}={x}\:+\frac{\mathrm{1}}{\mathrm{3}}\:{x}^{\mathrm{3}} \:+{o}\left({x}^{\mathrm{5}} \right)\Rightarrow\frac{{tanx}}{{x}}=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\:{x}^{\mathrm{2}} +{o}\left({x}^{\left.\mathrm{4}\right)} \right. \\ $$$${ln}\left(\frac{{tanx}}{{x}}\right)\sim{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{2}} \right)\sim\:\frac{\mathrm{1}}{\mathrm{3}}\:{x}^{\mathrm{2}} \:\:\:\:{x}\in{V}\left(\mathrm{0}\right) \\ $$$$\Rightarrow\:{lim}_{{x}\rightarrow\mathrm{0}\:} \:\:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:{ln}\left(\frac{{tanx}}{{x}}\right)\:\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\:{and} \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\left(\frac{{tanx}}{{x}}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} =^{\mathrm{3}} \sqrt{{e}}. \\ $$
