Question Number 27792 by abdo imad last updated on 14/Jan/18
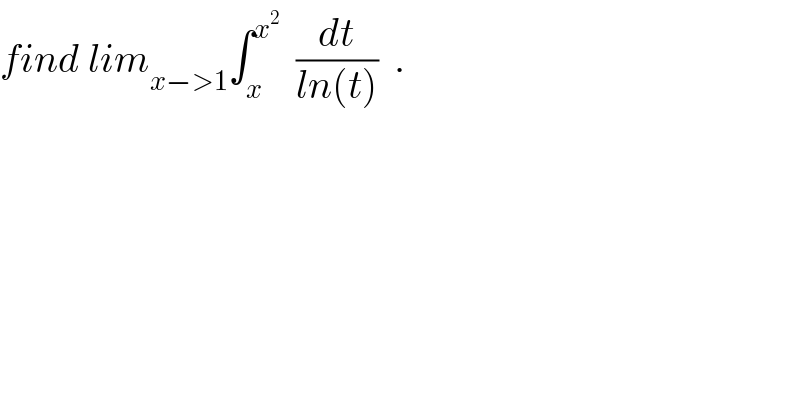
$${find}\:{lim}_{{x}−>\mathrm{1}} \int_{{x}} ^{{x}^{\mathrm{2}} } \:\:\frac{{dt}}{{ln}\left({t}\right)}\:\:. \\ $$
Commented by abdo imad last updated on 15/Jan/18
![if f continue in [a,b] and g integrable in [a,b]∃ c∈]a,b[/ ∫_a ^b f(x)g(x)dx= f(c) ∫_a ^b g(x)dx so ∃ c_x ∈]x,x^2 [ / ∫_x ^x^2 (dt/(lnt)) = (1/(ln c)) ∫_x ^x^2 dx = ((x^2 −x)/(lnc_x ))= ((x(x−1))/(ln(c_x )))but x−>1⇔c_x −>1 so lim_(x−>1) ∫_x ^x^2 (dt/(lnt))= lim_c_(x−>1) ((c_x (c_x ^ −1))/(lnc_x )) lim_c_(x−>1) (1/((lnc_x )/(c_x −1)))= 1 . (we can confuse x and c_x brcause x∈V(1) and c_x ∈ V(1).](https://www.tinkutara.com/question/Q27829.png)
$$\left.\:{if}\:{f}\:{continue}\:{in}\:\left[{a},{b}\right]\:{and}\:{g}\:{integrable}\:{in}\:\left[{a},{b}\right]\exists\:{c}\in\right]{a},{b}\left[/\right. \\ $$$$\left.\int_{{a}} ^{{b}} {f}\left({x}\right){g}\left({x}\right){dx}=\:{f}\left({c}\right)\:\int_{{a}} ^{{b}} {g}\left({x}\right){dx}\:\:\:{so}\:\:\exists\:{c}_{{x}} \:\in\right]{x},{x}^{\mathrm{2}} \left[\:/\right. \\ $$$$\int_{{x}} ^{{x}^{\mathrm{2}} } \:\frac{{dt}}{{lnt}}\:=\:\:\frac{\mathrm{1}}{{ln}\:{c}}\:\int_{{x}} ^{{x}^{\mathrm{2}} } {dx}\:=\:\frac{{x}^{\mathrm{2}} −{x}}{{lnc}_{{x}} }=\:\frac{{x}\left({x}−\mathrm{1}\right)}{{ln}\left({c}_{{x}} \:\right)}{but}\:{x}−>\mathrm{1}\Leftrightarrow{c}_{{x}} \:−>\mathrm{1} \\ $$$${so}\:{lim}_{{x}−>\mathrm{1}} \int_{{x}} ^{{x}^{\mathrm{2}} } \:\frac{{dt}}{{lnt}}=\:{lim}_{{c}_{{x}−>\mathrm{1}} } \:\:\frac{{c}_{{x}} \left({c}_{{x}} ^{} −\mathrm{1}\right)}{{lnc}_{{x}} } \\ $$$${lim}_{{c}_{{x}−>\mathrm{1}} } \:\:\:\:\:\frac{\mathrm{1}}{\frac{{lnc}_{{x}} }{{c}_{{x}} −\mathrm{1}}}=\:\mathrm{1}\:.\:\left({we}\:{can}\:{confuse}\:{x}\:{and}\:{c}_{{x}} \:{brcause}\right. \\ $$$${x}\in{V}\left(\mathrm{1}\right)\:{and}\:\:{c}_{{x}} \:\in\:{V}\left(\mathrm{1}\right). \\ $$
Commented by prakash jain last updated on 16/Jan/18

$$\mathrm{understood}\:\mathrm{rest}\:\mathrm{of}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{but} \\ $$$$\mathrm{What}\:\mathrm{is}\:{V}\left(\mathrm{1}\right)?\:\mathrm{is}\:\mathrm{it}\:\mathrm{vicinity}\:\mathrm{of}\:\mathrm{1}? \\ $$$$\mathrm{PS}:\:\mathrm{there}\:\mathrm{are}\:\mathrm{symbols}\:\mathrm{in}\:\mathrm{the}\:\mathrm{app}\:\mathrm{like} \\ $$$$\rightarrow,\infty\:\mathrm{which}\:\mathrm{you}\:\mathrm{can}\:\mathrm{use}\:\mathrm{press} \\ $$$$\mathrm{green}\:\int\:\mathrm{button}\:\mathrm{on}\:\mathrm{bottom}\:\mathrm{left}\:\mathrm{corner}. \\ $$
Commented by abdo imad last updated on 16/Jan/18
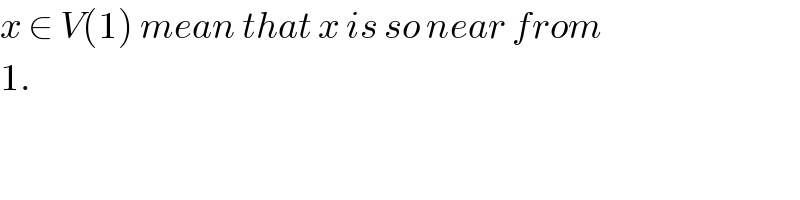
$${x}\:\in\:{V}\left(\mathrm{1}\right)\:{mean}\:{that}\:{x}\:{is}\:{so}\:{near}\:{from} \\ $$$$\mathrm{1}. \\ $$
