Question Number 52123 by 786786AM last updated on 03/Jan/19
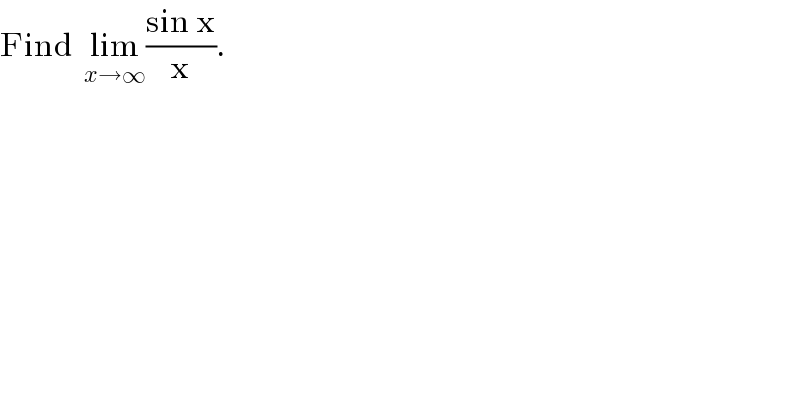
$$\mathrm{Find}\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}. \\ $$
Commented by turbo msup by abdo last updated on 03/Jan/19
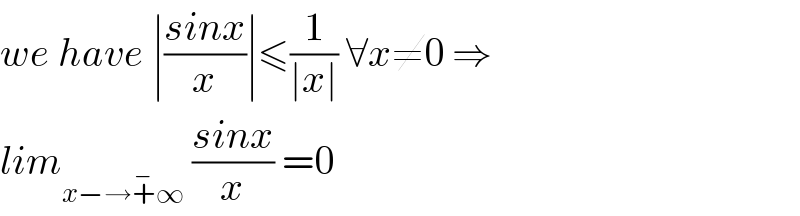
$${we}\:{have}\:\mid\frac{{sinx}}{{x}}\mid\leqslant\frac{\mathrm{1}}{\mid{x}\mid}\:\forall{x}\neq\mathrm{0}\:\Rightarrow \\ $$$${lim}_{{x}−\rightarrow\overset{−} {+}\infty} \:\frac{{sinx}}{{x}}\:=\mathrm{0} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Jan/19

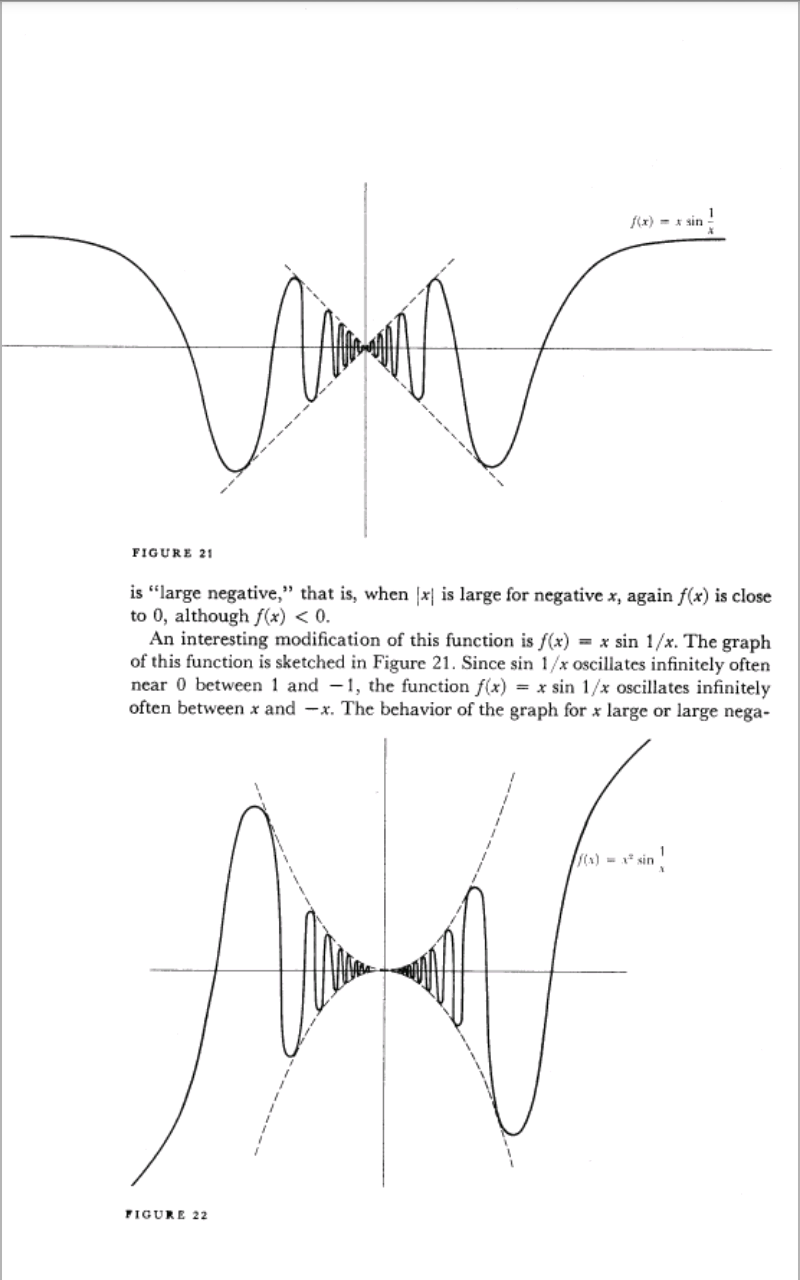
$${t}=\frac{\mathrm{1}}{{x}} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{tsin}\left(\frac{\mathrm{1}}{{t}}\right) \\ $$$${for}\:{any}\:{value}\:{of}\:{t}\:,{the}\:{value}\:{of}\:{sin}\left(\frac{\mathrm{1}}{{t}}\right)\:{oscillates} \\ $$$${between}\:\pm\mathrm{1}\:{so} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{t}×\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{sin}\left(\frac{\mathrm{1}}{{t}}\right) \\ $$$$=\mathrm{0}×\left(\pm\mathrm{1}\right) \\ $$$$=\mathrm{0} \\ $$$${i}\:{am}\:{attaching}\:{graph}\:{for}\:{the}\:{same}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 03/Jan/19

Commented by tanmay.chaudhury50@gmail.com last updated on 03/Jan/19