Question Number 30504 by abdo imad last updated on 22/Feb/18
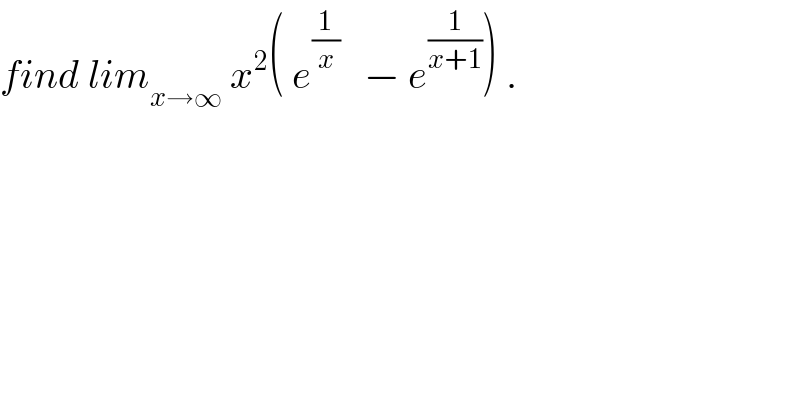
$${find}\:{lim}_{{x}\rightarrow\infty} \:{x}^{\mathrm{2}} \left(\:{e}^{\frac{\mathrm{1}}{{x}}} \:\:\:−\:{e}^{\frac{\mathrm{1}}{{x}+\mathrm{1}}} \right)\:. \\ $$
Answered by sma3l2996 last updated on 24/Feb/18
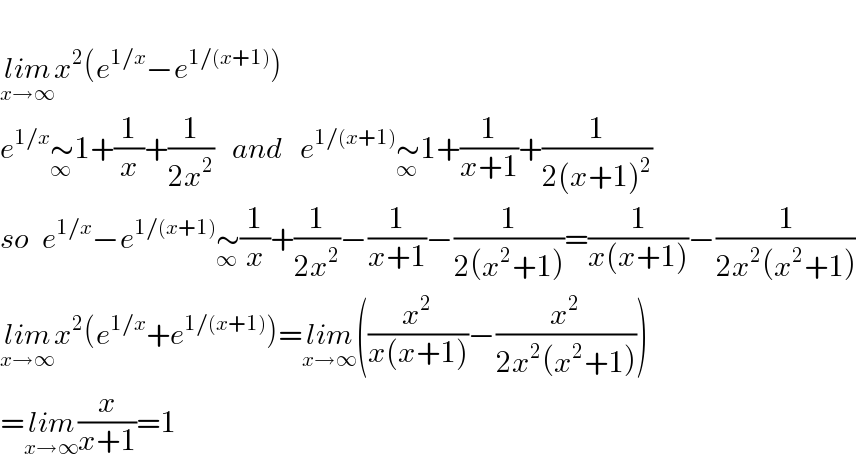
$$ \\ $$$$\underset{{x}\rightarrow\infty} {{lim}x}^{\mathrm{2}} \left({e}^{\mathrm{1}/{x}} −{e}^{\mathrm{1}/\left({x}+\mathrm{1}\right)} \right) \\ $$$${e}^{\mathrm{1}/{x}} \underset{\infty} {\sim}\mathrm{1}+\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\:\:\:{and}\:\:\:{e}^{\mathrm{1}/\left({x}+\mathrm{1}\right)} \underset{\infty} {\sim}\mathrm{1}+\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${so}\:\:{e}^{\mathrm{1}/{x}} −{e}^{\mathrm{1}/\left({x}+\mathrm{1}\right)} \underset{\infty} {\sim}\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\underset{{x}\rightarrow\infty} {{lim}x}^{\mathrm{2}} \left({e}^{\mathrm{1}/{x}} +{e}^{\mathrm{1}/\left({x}+\mathrm{1}\right)} \right)=\underset{{x}\rightarrow\infty} {{lim}}\left(\frac{{x}^{\mathrm{2}} }{{x}\left({x}+\mathrm{1}\right)}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)}\right) \\ $$$$=\underset{{x}\rightarrow\infty} {{lim}}\frac{{x}}{{x}+\mathrm{1}}=\mathrm{1} \\ $$
