Menu Close

find-ln-1-x-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 47720 by maxmathsup by imad last updated on 13/Nov/18
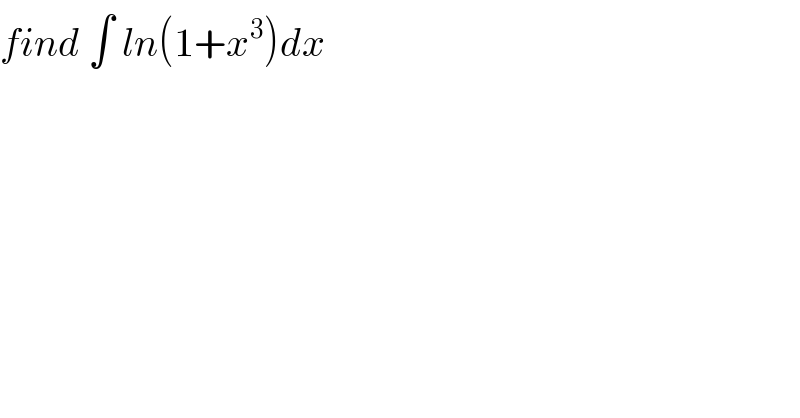
find ∫ ln(1+x^3 )dx
$${find}\:\int\:{ln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right){dx} \\ $$
Answered by MJS last updated on 14/Nov/18
∫ln (x^3 +1) dx= [((in parts:)),((u′=1 → u=x)),((v=ln (x^3 +1) → v′=((3x^2 )/(x^3 +1)))) ] =xln (x^3 +1) −∫((3x^3 )/(x^3 +1))dx ∫(x^3 /(x^3 +1))dx=∫(1−(1/(x^3 +1)))dx=x−∫(dx/(x^3 +1)) ∫(dx/(x^3 +1))=∫(dx/((x+1)(x^2 −x+1)))=(1/3)∫(dx/(x+1))−(1/3)∫((x−2)/(x^2 −x+1))dx= =(1/3)∫(dx/(x+1))−(1/3)∫(((2x−1)/(2(x^2 −x+1)))−(3/(2(x^2 −x+1))))dx= =(1/3)∫(dx/(x+1))−(1/6)∫((2x−1)/(x^2 −x+1))dx+(1/2)∫(dx/(x^2 −x+1)) ∫(dx/(x+1))=ln (x+1) ∫((2x−1)/(x^2 −x+1))dx=ln (x^2 −x+1) ∫(dx/(x^2 −x+1))=∫(dx/((x−(1/2))^2 +(3/4)))= [((t=((2(√3))/3)x−((√3)/3) → dx=((√3)/2)dt)) ] =((2(√3))/3)∫(dt/(t^2 +1))=((2(√3))/3)arctan t =((2(√3))/2)arctan (((2(√3))/3)x−((√3)/3)) ∫ln (x^3 +1) dx=−3x+(√3)arctan (((2(√3))/3)x−((√3)/3))+xln ∣x^3 +1∣ −(1/2)ln ∣x^2 −x+1∣ +ln ∣x+1∣ +C
$$\int\mathrm{ln}\:\left({x}^{\mathrm{3}} +\mathrm{1}\right)\:{dx}= \\ $$$$\:\:\:\:\:\begin{bmatrix}{\mathrm{in}\:\mathrm{parts}:}\\{{u}'=\mathrm{1}\:\rightarrow\:{u}={x}}\\{{v}=\mathrm{ln}\:\left({x}^{\mathrm{3}} +\mathrm{1}\right)\:\rightarrow\:{v}'=\frac{\mathrm{3}{x}^{\mathrm{2}} }{{x}^{\mathrm{3}} +\mathrm{1}}}\end{bmatrix} \\ $$$$={x}\mathrm{ln}\:\left({x}^{\mathrm{3}} +\mathrm{1}\right)\:−\int\frac{\mathrm{3}{x}^{\mathrm{3}} }{{x}^{\mathrm{3}} +\mathrm{1}}{dx} \\ $$$$\int\frac{{x}^{\mathrm{3}} }{{x}^{\mathrm{3}} +\mathrm{1}}{dx}=\int\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{3}} +\mathrm{1}}\right){dx}={x}−\int\frac{{dx}}{{x}^{\mathrm{3}} +\mathrm{1}} \\ $$$$ \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{3}} +\mathrm{1}}=\int\frac{{dx}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}\int\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}−\frac{\mathrm{3}}{\mathrm{2}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}\right){dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{6}}\int\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$$ \\ $$$$\int\frac{{dx}}{{x}+\mathrm{1}}=\mathrm{ln}\:\left({x}+\mathrm{1}\right) \\ $$$$\int\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}=\mathrm{ln}\:\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right) \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}=\int\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}= \\ $$$$\:\:\:\:\:\begin{bmatrix}{{t}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}{x}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt}}\end{bmatrix} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:{t}\:=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{arctan}\:\left(\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}{x}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right) \\ $$$$ \\ $$$$\int\mathrm{ln}\:\left({x}^{\mathrm{3}} +\mathrm{1}\right)\:{dx}=−\mathrm{3}{x}+\sqrt{\mathrm{3}}\mathrm{arctan}\:\left(\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}{x}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right)+{x}\mathrm{ln}\:\mid{x}^{\mathrm{3}} +\mathrm{1}\mid\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid{x}^{\mathrm{2}} −{x}+\mathrm{1}\mid\:+\mathrm{ln}\:\mid{x}+\mathrm{1}\mid\:+{C} \\ $$
Commented by maxmathsup by imad last updated on 15/Nov/18
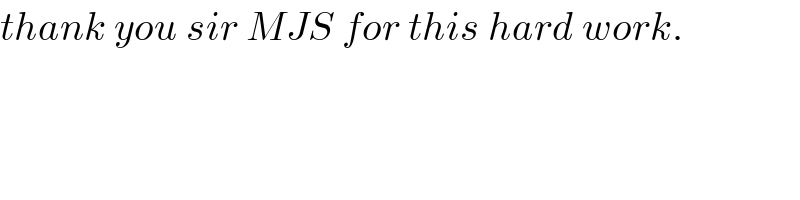
thank you sir MJS for this hard work.
$${thank}\:{you}\:{sir}\:{MJS}\:{for}\:{this}\:{hard}\:{work}. \\ $$
Answered by Smail last updated on 14/Nov/18
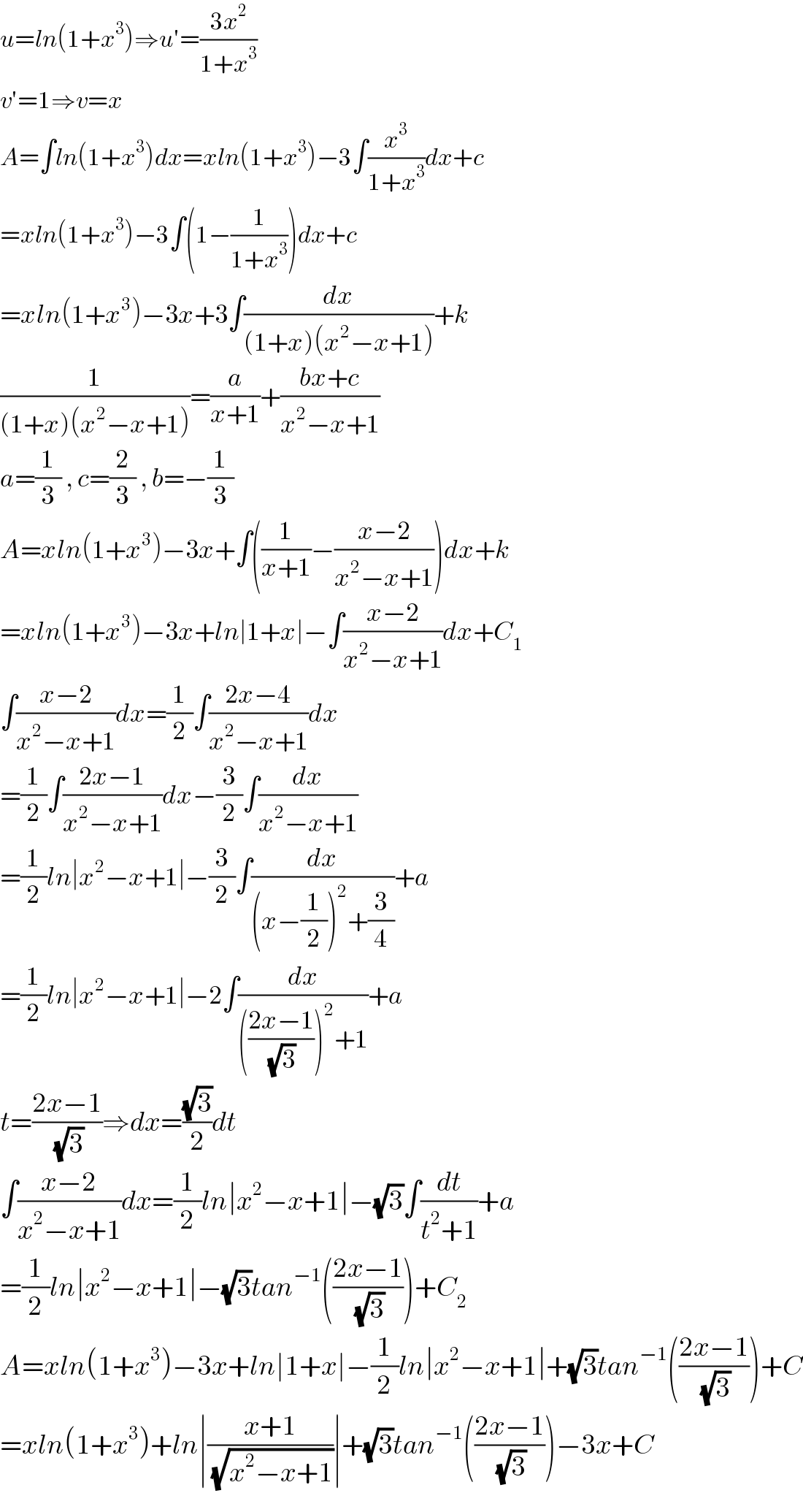
u=ln(1+x^3 )⇒u′=((3x^2 )/(1+x^3 )) v′=1⇒v=x A=∫ln(1+x^3 )dx=xln(1+x^3 )−3∫(x^3 /(1+x^3 ))dx+c =xln(1+x^3 )−3∫(1−(1/(1+x^3 )))dx+c =xln(1+x^3 )−3x+3∫(dx/((1+x)(x^2 −x+1)))+k (1/((1+x)(x^2 −x+1)))=(a/(x+1))+((bx+c)/(x^2 −x+1)) a=(1/3) , c=(2/3) , b=−(1/3) A=xln(1+x^3 )−3x+∫((1/(x+1))−((x−2)/(x^2 −x+1)))dx+k =xln(1+x^3 )−3x+ln∣1+x∣−∫((x−2)/(x^2 −x+1))dx+C_1 ∫((x−2)/(x^2 −x+1))dx=(1/2)∫((2x−4)/(x^2 −x+1))dx =(1/2)∫((2x−1)/(x^2 −x+1))dx−(3/2)∫(dx/(x^2 −x+1)) =(1/2)ln∣x^2 −x+1∣−(3/2)∫(dx/((x−(1/2))^2 +(3/4)))+a =(1/2)ln∣x^2 −x+1∣−2∫(dx/((((2x−1)/( (√3))))^2 +1))+a t=((2x−1)/( (√3)))⇒dx=((√3)/2)dt ∫((x−2)/(x^2 −x+1))dx=(1/2)ln∣x^2 −x+1∣−(√3)∫(dt/(t^2 +1))+a =(1/2)ln∣x^2 −x+1∣−(√3)tan^(−1) (((2x−1)/( (√3))))+C_2 A=xln(1+x^3 )−3x+ln∣1+x∣−(1/2)ln∣x^2 −x+1∣+(√3)tan^(−1) (((2x−1)/( (√3))))+C =xln(1+x^3 )+ln∣((x+1)/( (√(x^2 −x+1))))∣+(√3)tan^(−1) (((2x−1)/( (√3))))−3x+C
$${u}={ln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)\Rightarrow{u}'=\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{3}} } \\ $$$${v}'=\mathrm{1}\Rightarrow{v}={x} \\ $$$${A}=\int{ln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right){dx}={xln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)−\mathrm{3}\int\frac{{x}^{\mathrm{3}} }{\mathrm{1}+{x}^{\mathrm{3}} }{dx}+{c} \\ $$$$={xln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)−\mathrm{3}\int\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{3}} }\right){dx}+{c} \\ $$$$={xln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)−\mathrm{3}{x}+\mathrm{3}\int\frac{{dx}}{\left(\mathrm{1}+{x}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}+{k} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}=\frac{{a}}{{x}+\mathrm{1}}+\frac{{bx}+{c}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{3}}\:,\:{c}=\frac{\mathrm{2}}{\mathrm{3}}\:,\:{b}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${A}={xln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)−\mathrm{3}{x}+\int\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}−\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\right){dx}+{k} \\ $$$$={xln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)−\mathrm{3}{x}+{ln}\mid\mathrm{1}+{x}\mid−\int\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}+{C}_{\mathrm{1}} \\ $$$$\int\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}−\mathrm{4}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} −{x}+\mathrm{1}\mid−\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}+{a} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} −{x}+\mathrm{1}\mid−\mathrm{2}\int\frac{{dx}}{\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} +\mathrm{1}}+{a} \\ $$$${t}=\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\Rightarrow{dx}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt} \\ $$$$\int\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} −{x}+\mathrm{1}\mid−\sqrt{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}+{a} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} −{x}+\mathrm{1}\mid−\sqrt{\mathrm{3}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+{C}_{\mathrm{2}} \\ $$$${A}={xln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)−\mathrm{3}{x}+{ln}\mid\mathrm{1}+{x}\mid−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{x}^{\mathrm{2}} −{x}+\mathrm{1}\mid+\sqrt{\mathrm{3}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+{C} \\ $$$$={xln}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)+{ln}\mid\frac{{x}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}\mid+\sqrt{\mathrm{3}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)−\mathrm{3}{x}+{C} \\ $$
Commented by maxmathsup by imad last updated on 15/Nov/18
thank you sir.
$${thank}\:{you}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *