Question Number 153105 by alisiao last updated on 04/Sep/21
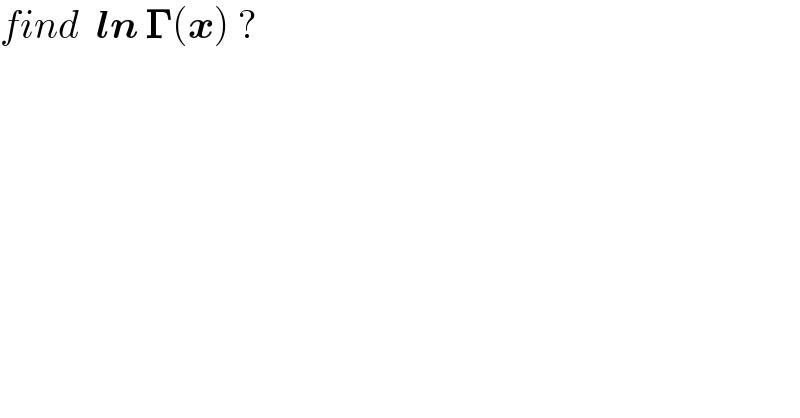
$${find}\:\:\boldsymbol{{ln}}\:\boldsymbol{\Gamma}\left(\boldsymbol{{x}}\right)\:? \\ $$
Answered by puissant last updated on 04/Sep/21
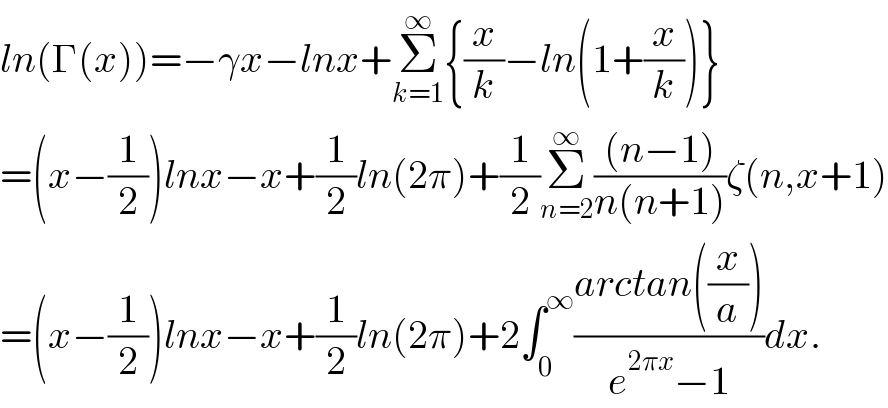
$${ln}\left(\Gamma\left({x}\right)\right)=−\gamma{x}−{lnx}+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left\{\frac{{x}}{{k}}−{ln}\left(\mathrm{1}+\frac{{x}}{{k}}\right)\right\} \\ $$$$=\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right){lnx}−{x}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\pi\right)+\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left({n}−\mathrm{1}\right)}{{n}\left({n}+\mathrm{1}\right)}\zeta\left({n},{x}+\mathrm{1}\right) \\ $$$$=\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right){lnx}−{x}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\pi\right)+\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{arctan}\left(\frac{{x}}{{a}}\right)}{{e}^{\mathrm{2}\pi{x}} −\mathrm{1}}{dx}. \\ $$
