Question Number 38719 by maxmathsup by imad last updated on 28/Jun/18
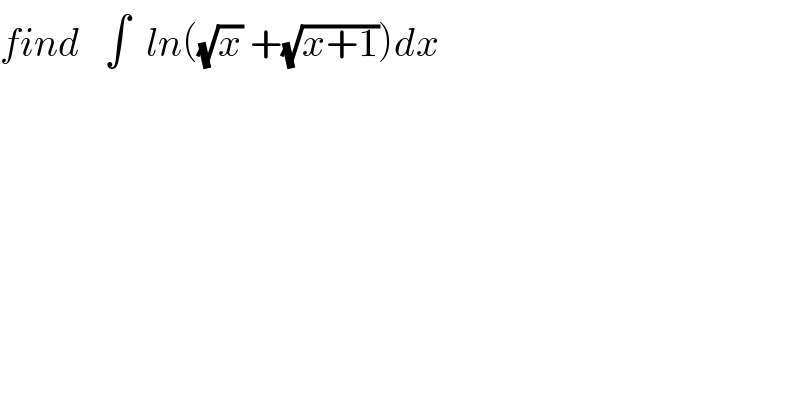
$${find}\:\:\:\int\:\:{ln}\left(\sqrt{{x}}\:+\sqrt{{x}+\mathrm{1}}\right){dx} \\ $$
Answered by behi83417@gmail.com last updated on 29/Jun/18
![I=xln((√x)+(√(x+1)))−∫x(((1/(2(√x)))+(1/(2(√(x+1)))))/( (√x)+(√(x+1))))dx= =do−∫(x/(2(√x)(√(x+1))))dx=do−∫((√x)/(2(√(x+1))))dx x=tg^2 t⇒dx=2tgt(1+tg^2 t)dt ⇒∫((√x)/( (√(x+1))))dx=∫((tgt.2tgt(1+tg^2 t)dt)/(sect))= =∫2tg^2 t.sectdt=2∫(sec^2 t−1)sectdt= =2∫(sec^3 t−sect)dt= =2(((sect.tgt)/2)+(1/2)∫sectdt−∫sectdt)= =sect.tgt−ln(sect+tgt)+const ⇒I=x.ln((√x)+(√(x+1)))−(1/2)(√x).(√(x+1))− −(1/2)ln((√x)+(√(x+1)))+const. ■ I=(1/2)[(2x−1).ln((√x)+(√(x+1)))−(√(x^2 +x))]+const.](https://www.tinkutara.com/question/Q38791.png)
$${I}={xln}\left(\sqrt{{x}}+\sqrt{{x}+\mathrm{1}}\right)−\int{x}\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}+\mathrm{1}}}}{\:\sqrt{{x}}+\sqrt{{x}+\mathrm{1}}}{dx}= \\ $$$$={do}−\int\frac{{x}}{\mathrm{2}\sqrt{{x}}\sqrt{{x}+\mathrm{1}}}{dx}={do}−\int\frac{\sqrt{{x}}}{\mathrm{2}\sqrt{{x}+\mathrm{1}}}{dx} \\ $$$${x}={tg}^{\mathrm{2}} {t}\Rightarrow{dx}=\mathrm{2}{tgt}\left(\mathrm{1}+{tg}^{\mathrm{2}} {t}\right){dt} \\ $$$$\Rightarrow\int\frac{\sqrt{{x}}}{\:\sqrt{{x}+\mathrm{1}}}{dx}=\int\frac{{tgt}.\mathrm{2}{tgt}\left(\mathrm{1}+{tg}^{\mathrm{2}} {t}\right){dt}}{{sect}}= \\ $$$$=\int\mathrm{2}{tg}^{\mathrm{2}} {t}.{sectdt}=\mathrm{2}\int\left({sec}^{\mathrm{2}} {t}−\mathrm{1}\right){sectdt}= \\ $$$$=\mathrm{2}\int\left({sec}^{\mathrm{3}} {t}−{sect}\right){dt}= \\ $$$$=\mathrm{2}\left(\frac{{sect}.{tgt}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\int{sectdt}−\int{sectdt}\right)= \\ $$$$={sect}.{tgt}−{ln}\left({sect}+{tgt}\right)+{const} \\ $$$$\Rightarrow{I}=\boldsymbol{{x}}.\boldsymbol{{ln}}\left(\sqrt{\boldsymbol{{x}}}+\sqrt{\boldsymbol{{x}}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\boldsymbol{{x}}}.\sqrt{\boldsymbol{{x}}+\mathrm{1}}− \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{ln}}\left(\sqrt{\boldsymbol{{x}}}+\sqrt{\boldsymbol{{x}}+\mathrm{1}}\right)+\boldsymbol{{const}}.\:\blacksquare \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\mathrm{2}{x}−\mathrm{1}\right).{ln}\left(\sqrt{{x}}+\sqrt{{x}+\mathrm{1}}\right)−\sqrt{{x}^{\mathrm{2}} +{x}}\right]+{const}. \\ $$
Commented by maxmathsup by imad last updated on 30/Jun/18
$${thank}\:{you}\:{sir}\:{Behi}. \\ $$
