Question Number 36430 by prof Abdo imad last updated on 02/Jun/18
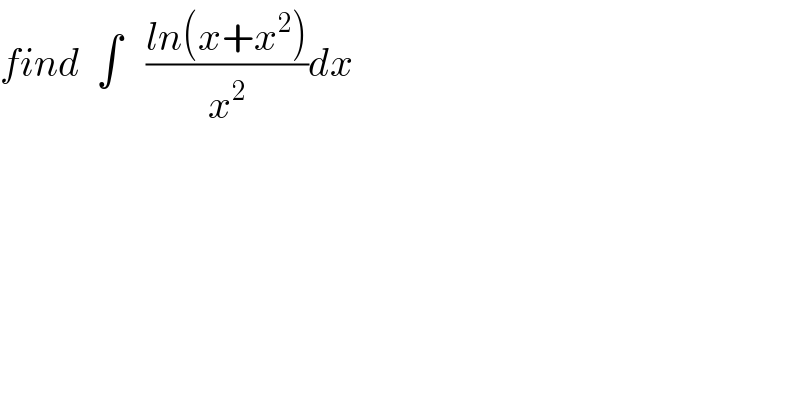
$${find}\:\:\int\:\:\:\frac{{ln}\left({x}+{x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} }{dx}\: \\ $$
Commented by abdo mathsup last updated on 03/Jun/18
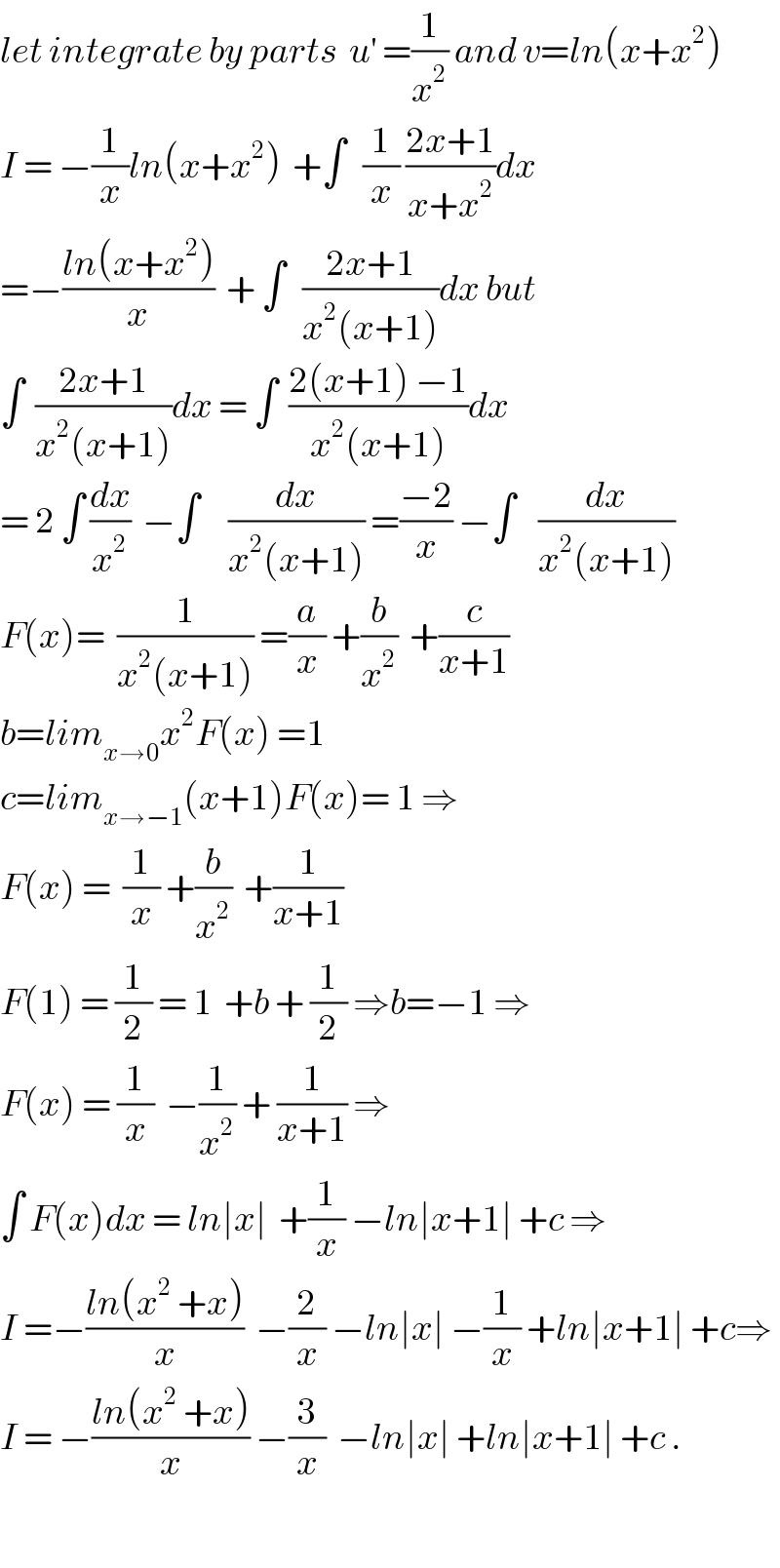
$${let}\:{integrate}\:{by}\:{parts}\:\:{u}^{'} \:=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:{and}\:{v}={ln}\left({x}+{x}^{\mathrm{2}} \right) \\ $$$${I}\:=\:−\frac{\mathrm{1}}{{x}}{ln}\left({x}+{x}^{\mathrm{2}} \right)\:\:+\int\:\:\:\frac{\mathrm{1}}{{x}}\:\frac{\mathrm{2}{x}+\mathrm{1}}{{x}+{x}^{\mathrm{2}} }{dx} \\ $$$$=−\frac{{ln}\left({x}+{x}^{\mathrm{2}} \right)}{{x}}\:\:+\:\int\:\:\:\frac{\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}{dx}\:{but} \\ $$$$\int\:\:\frac{\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}{dx}\:=\:\int\:\:\frac{\mathrm{2}\left({x}+\mathrm{1}\right)\:−\mathrm{1}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}{dx} \\ $$$$=\:\mathrm{2}\:\int\:\frac{{dx}}{{x}^{\mathrm{2}} }\:\:−\int\:\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}\:=\frac{−\mathrm{2}}{{x}}\:−\int\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)} \\ $$$${F}\left({x}\right)=\:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}\:=\frac{{a}}{{x}}\:+\frac{{b}}{{x}^{\mathrm{2}} }\:\:+\frac{{c}}{{x}+\mathrm{1}} \\ $$$${b}={lim}_{{x}\rightarrow\mathrm{0}} {x}^{\mathrm{2}} {F}\left({x}\right)\:=\mathrm{1}\: \\ $$$${c}={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right){F}\left({x}\right)=\:\mathrm{1}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\:\:\frac{\mathrm{1}}{{x}}\:+\frac{{b}}{{x}^{\mathrm{2}} }\:\:+\frac{\mathrm{1}}{{x}+\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:=\:\mathrm{1}\:\:+{b}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{b}=−\mathrm{1}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\:\frac{\mathrm{1}}{{x}}\:\:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{{x}+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:{F}\left({x}\right){dx}\:=\:{ln}\mid{x}\mid\:\:+\frac{\mathrm{1}}{{x}}\:−{ln}\mid{x}+\mathrm{1}\mid\:+{c}\:\Rightarrow \\ $$$${I}\:=−\frac{{ln}\left({x}^{\mathrm{2}} \:+{x}\right)}{{x}}\:\:−\frac{\mathrm{2}}{{x}}\:−{ln}\mid{x}\mid\:−\frac{\mathrm{1}}{{x}}\:+{ln}\mid{x}+\mathrm{1}\mid\:+{c}\Rightarrow \\ $$$${I}\:=\:−\frac{{ln}\left({x}^{\mathrm{2}} \:+{x}\right)}{{x}}\:−\frac{\mathrm{3}}{{x}}\:\:−{ln}\mid{x}\mid\:+{ln}\mid{x}+\mathrm{1}\mid\:+{c}\:. \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 02/Jun/18
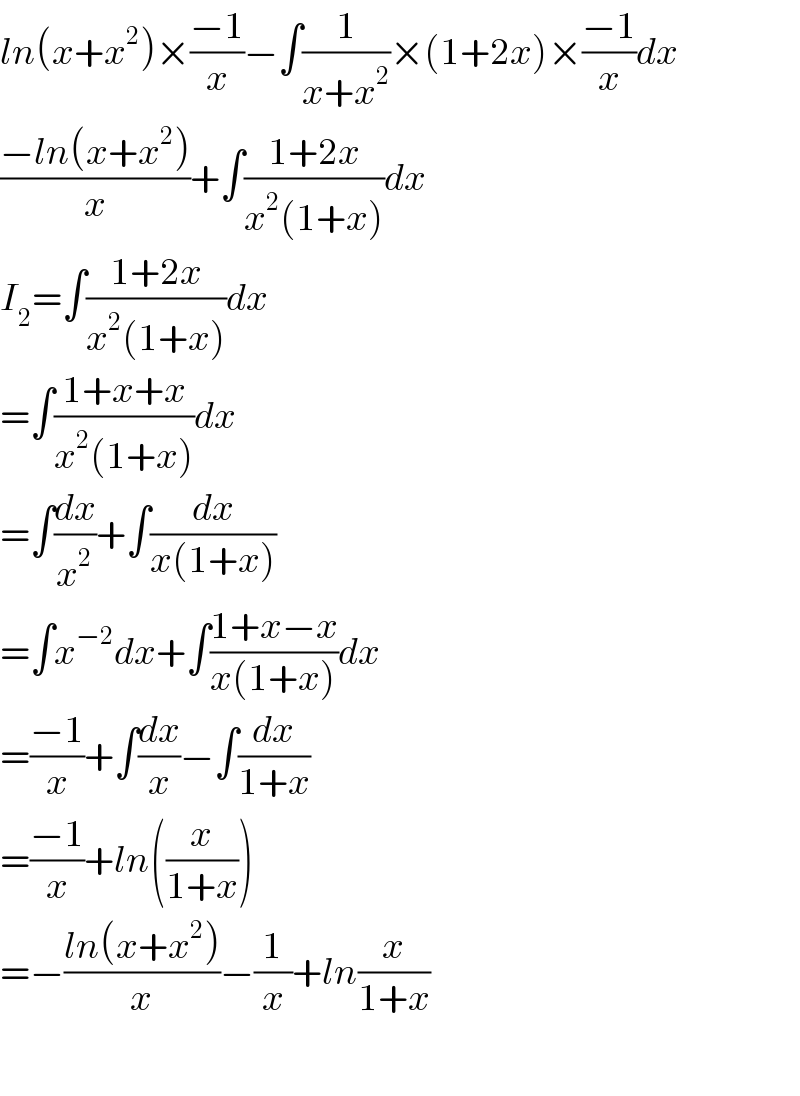
$${ln}\left({x}+{x}^{\mathrm{2}} \right)×\frac{−\mathrm{1}}{{x}}−\int\frac{\mathrm{1}}{{x}+{x}^{\mathrm{2}} }×\left(\mathrm{1}+\mathrm{2}{x}\right)×\frac{−\mathrm{1}}{{x}}{dx} \\ $$$$\frac{−{ln}\left({x}+{x}^{\mathrm{2}} \right)}{{x}}+\int\frac{\mathrm{1}+\mathrm{2}{x}}{{x}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)}{dx} \\ $$$${I}_{\mathrm{2}} =\int\frac{\mathrm{1}+\mathrm{2}{x}}{{x}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)}{dx} \\ $$$$=\int\frac{\mathrm{1}+{x}+{x}}{{x}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)}{dx} \\ $$$$=\int\frac{{dx}}{{x}^{\mathrm{2}} }+\int\frac{{dx}}{{x}\left(\mathrm{1}+{x}\right)} \\ $$$$=\int{x}^{−\mathrm{2}} {dx}+\int\frac{\mathrm{1}+{x}−{x}}{{x}\left(\mathrm{1}+{x}\right)}{dx} \\ $$$$=\frac{−\mathrm{1}}{{x}}+\int\frac{{dx}}{{x}}−\int\frac{{dx}}{\mathrm{1}+{x}} \\ $$$$=\frac{−\mathrm{1}}{{x}}+{ln}\left(\frac{{x}}{\mathrm{1}+{x}}\right) \\ $$$$=−\frac{{ln}\left({x}+{x}^{\mathrm{2}} \right)}{{x}}−\frac{\mathrm{1}}{{x}}+{ln}\frac{{x}}{\mathrm{1}+{x}} \\ $$$$ \\ $$
