Question Number 57960 by mr W last updated on 15/Apr/19
$${Find}\:{maximum}\:{n}\:{such}\:{that}\:\mathrm{12}^{{n}} \:{divides} \\ $$$$\mathrm{100}!. \\ $$
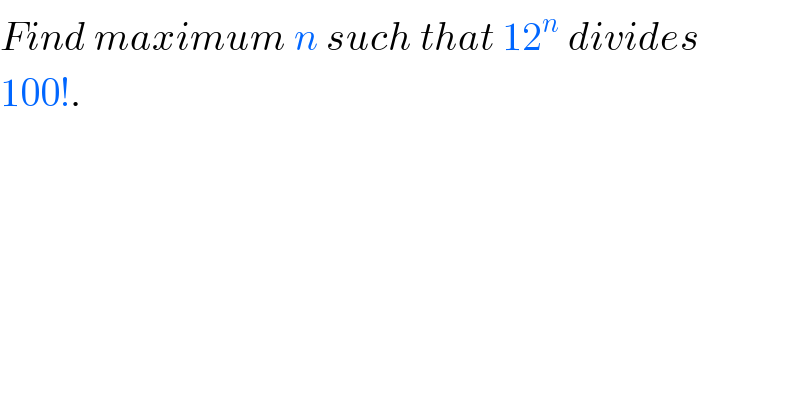
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Apr/19
![12=3×2^2 highest power of 3 contained in 100! is I[((100)/3)]+I[((100)/3^2 )]+I[((100)/3^3 )]+I[((100)/3^4 )] =33+11+3+1 =48 higest power of 2 contained in 100! I[((100)/2)]+I[((100)/2^2 )]+I[((100)/2^3 )]+[((100)/2^4 )]+I[((100)/2^5 )]+I[((100)/2^6 )] =50+25+12+6+3+1 =97 so highest power of 12→12^n the value of n=48 [common minimum value between highest power of factor 3 and 2] sir pls check...](https://www.tinkutara.com/question/Q57961.png)
$$\mathrm{12}=\mathrm{3}×\mathrm{2}^{\mathrm{2}} \\ $$$${highest}\:{power}\:{of}\:\mathrm{3}\:{contained}\:{in}\:\mathrm{100}!\:{is} \\ $$$${I}\left[\frac{\mathrm{100}}{\mathrm{3}}\right]+{I}\left[\frac{\mathrm{100}}{\mathrm{3}^{\mathrm{2}} }\right]+{I}\left[\frac{\mathrm{100}}{\mathrm{3}^{\mathrm{3}} }\right]+{I}\left[\frac{\mathrm{100}}{\mathrm{3}^{\mathrm{4}} }\right] \\ $$$$=\mathrm{33}+\mathrm{11}+\mathrm{3}+\mathrm{1} \\ $$$$=\mathrm{48} \\ $$$${higest}\:{power}\:{of}\:\mathrm{2}\:{contained}\:{in}\:\mathrm{100}! \\ $$$${I}\left[\frac{\mathrm{100}}{\mathrm{2}}\right]+{I}\left[\frac{\mathrm{100}}{\mathrm{2}^{\mathrm{2}} }\right]+{I}\left[\frac{\mathrm{100}}{\mathrm{2}^{\mathrm{3}} }\right]+\left[\frac{\mathrm{100}}{\mathrm{2}^{\mathrm{4}} }\right]+{I}\left[\frac{\mathrm{100}}{\mathrm{2}^{\mathrm{5}} }\right]+{I}\left[\frac{\mathrm{100}}{\mathrm{2}^{\mathrm{6}} }\right] \\ $$$$=\mathrm{50}+\mathrm{25}+\mathrm{12}+\mathrm{6}+\mathrm{3}+\mathrm{1} \\ $$$$=\mathrm{97} \\ $$$${so}\:{highest}\:{power}\:{of}\:\mathrm{12}\rightarrow\mathrm{12}^{{n}} \\ $$$${the}\:{value}\:{of}\:{n}=\mathrm{48}\:\left[{common}\:{minimum}\:{value}\right. \\ $$$$\left.{between}\:{highest}\:{power}\:{of}\:{factor}\:\mathrm{3}\:{and}\:\mathrm{2}\right] \\ $$$${sir}\:{pls}\:{check}… \\ $$$$ \\ $$
Commented by mr W last updated on 15/Apr/19
$${correct},\:{thank}\:{you}\:{very}\:{much}\:{sir}! \\ $$
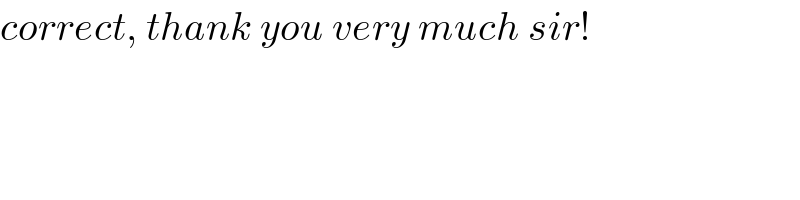
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Apr/19
$${most}\:{welcome}\:{sir} \\ $$
Commented by mr W last updated on 15/Apr/19
$${the}\:{answer}\:{is}\:{an}\:{other}\:{if}\:{the}\:{question} \\ $$$${is}\:{not}\:\mathrm{100}!\:{but}\:\mathrm{99}!.\:{am}\:{i}\:{right}? \\ $$
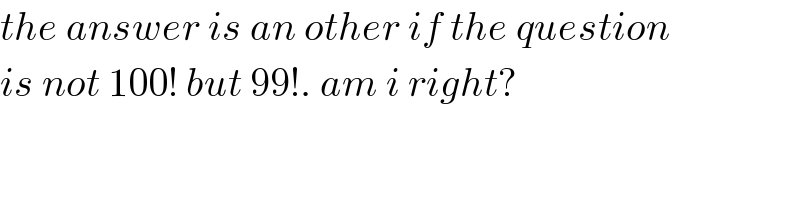
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Apr/19
![I[((99)/3)]+I[((99)/3^2 )]+I[((99)/3^3 )]+I[((99)/3^4 )] =33+11+3+1=48 I[((99)/2)]+I[((99)/2^2 )]+I[((99)/2^3 )]+I[((99)/2^4 )]+I[((99)/2^5 )]+I[((99)/2^6 )] =49+24+12+6+3+1 =95 so ans is 48 ...sir pls chdck](https://www.tinkutara.com/question/Q57973.png)
$${I}\left[\frac{\mathrm{99}}{\mathrm{3}}\right]+{I}\left[\frac{\mathrm{99}}{\mathrm{3}^{\mathrm{2}} }\right]+{I}\left[\frac{\mathrm{99}}{\mathrm{3}^{\mathrm{3}} }\right]+{I}\left[\frac{\mathrm{99}}{\mathrm{3}^{\mathrm{4}} }\right] \\ $$$$=\mathrm{33}+\mathrm{11}+\mathrm{3}+\mathrm{1}=\mathrm{48} \\ $$$${I}\left[\frac{\mathrm{99}}{\mathrm{2}}\right]+{I}\left[\frac{\mathrm{99}}{\mathrm{2}^{\mathrm{2}} }\right]+{I}\left[\frac{\mathrm{99}}{\mathrm{2}^{\mathrm{3}} }\right]+{I}\left[\frac{\mathrm{99}}{\mathrm{2}^{\mathrm{4}} }\right]+{I}\left[\frac{\mathrm{99}}{\mathrm{2}^{\mathrm{5}} }\right]+{I}\left[\frac{\mathrm{99}}{\mathrm{2}^{\mathrm{6}} }\right] \\ $$$$=\mathrm{49}+\mathrm{24}+\mathrm{12}+\mathrm{6}+\mathrm{3}+\mathrm{1} \\ $$$$=\mathrm{95} \\ $$$${so}\:{ans}\:{is}\:\mathrm{48}\:…{sir}\:{pls}\:{chdck} \\ $$$$ \\ $$
Commented by mr W last updated on 15/Apr/19
$$\mathrm{12}^{{n}} =\mathrm{3}^{{n}} ×\mathrm{2}^{\mathrm{2}{n}} \\ $$$${for}\:{power}\:{of}\:\mathrm{3}:\:{n}\leqslant\mathrm{48} \\ $$$${for}\:{power}\:{of}\:\mathrm{2}:\:\mathrm{2}{n}\leqslant\mathrm{95}\:\Rightarrow\:{n}\leqslant\mathrm{47} \\ $$$$\Rightarrow{n}_{{max}} =\mathrm{47} \\ $$
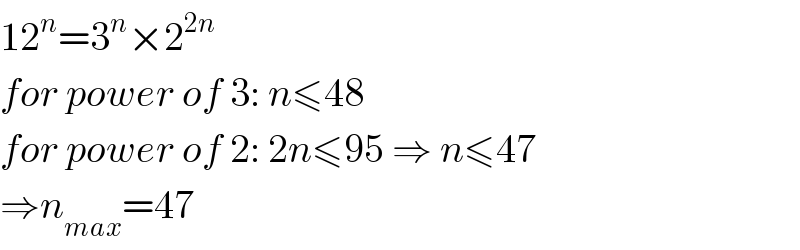
Commented by tanmay.chaudhury50@gmail.com last updated on 15/Apr/19
$${yes}\:{sir}\:{thank}\:{you}\:{for}\:{your}\:{thought}\:{process} \\ $$$${quite}\:{deep}\:…{thanks}\:{again}… \\ $$