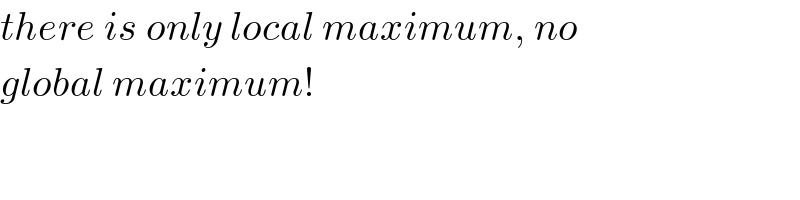Find-minimum-and-maximum-of-f-x-9x-2-sin-2-x-4-x-sin-x-where-0-lt-x-lt-pi-

Question Number 124557 by bemath last updated on 04/Dec/20

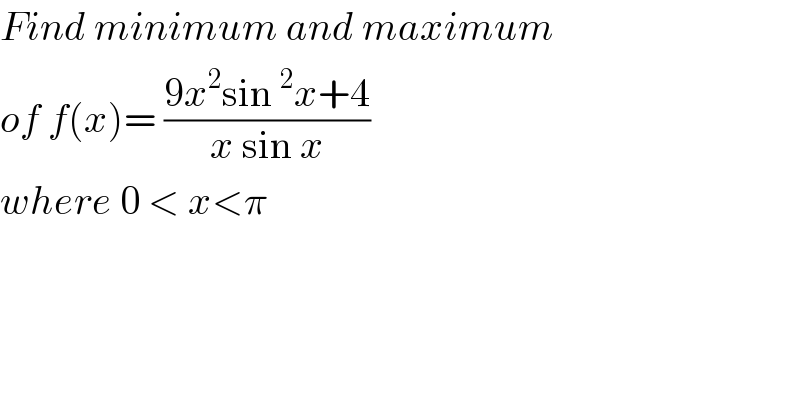
Find minimum and maximum of f(x)= ((9x^2 sin^2 x+4)/(x sin x)) where 0 < x<π

$${Find}\:{minimum}\:{and}\:{maximum} \\ $$$${of}\:{f}\left({x}\right)=\:\frac{\mathrm{9}{x}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{4}}{{x}\:\mathrm{sin}\:{x}} \\ $$$${where}\:\mathrm{0}\:<\:{x}<\pi \\ $$

Answered by mr W last updated on 04/Dec/20

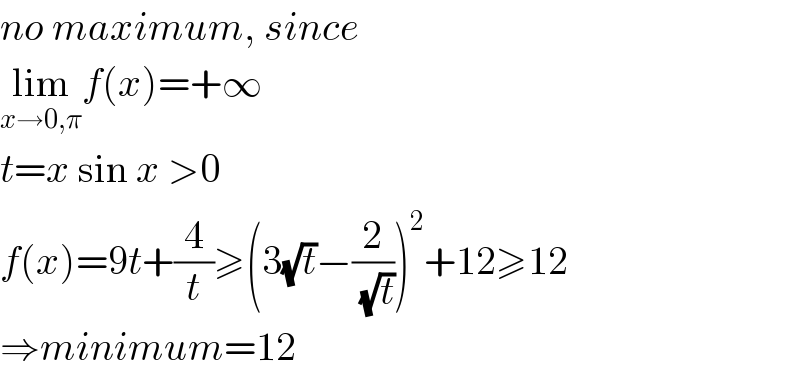
no maximum, since lim_(x→0,π) f(x)=+∞ t=x sin x >0 f(x)=9t+(4/t)≥(3(√t)−(2/( (√t))))^2 +12≥12 ⇒minimum=12

$${no}\:{maximum},\:{since} \\ $$$$\underset{{x}\rightarrow\mathrm{0},\pi} {\mathrm{lim}}{f}\left({x}\right)=+\infty \\ $$$${t}={x}\:\mathrm{sin}\:{x}\:>\mathrm{0} \\ $$$${f}\left({x}\right)=\mathrm{9}{t}+\frac{\mathrm{4}}{{t}}\geqslant\left(\mathrm{3}\sqrt{{t}}−\frac{\mathrm{2}}{\:\sqrt{{t}}}\right)^{\mathrm{2}} +\mathrm{12}\geqslant\mathrm{12} \\ $$$$\Rightarrow{minimum}=\mathrm{12} \\ $$

Commented by bemath last updated on 04/Dec/20