Question Number 89805 by jagoll last updated on 19/Apr/20
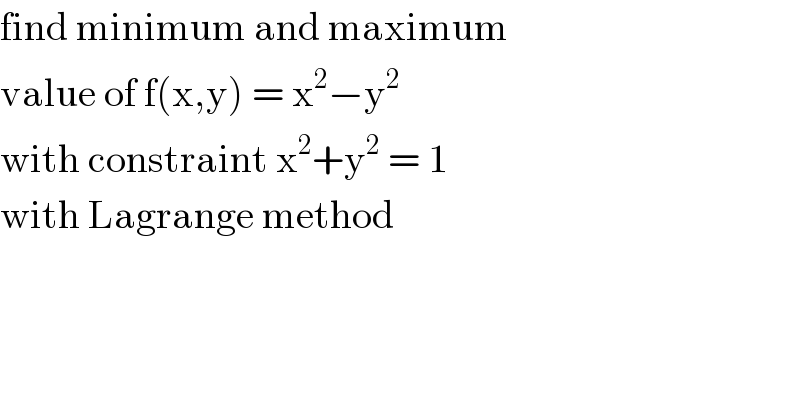
$$\mathrm{find}\:\mathrm{minimum}\:\mathrm{and}\:\mathrm{maximum} \\ $$$$\mathrm{value}\:\mathrm{of}\:\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)\:=\:\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{with}\:\mathrm{constraint}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{1} \\ $$$$\mathrm{with}\:\mathrm{Lagrange}\:\mathrm{method} \\ $$
Commented by john santu last updated on 19/Apr/20
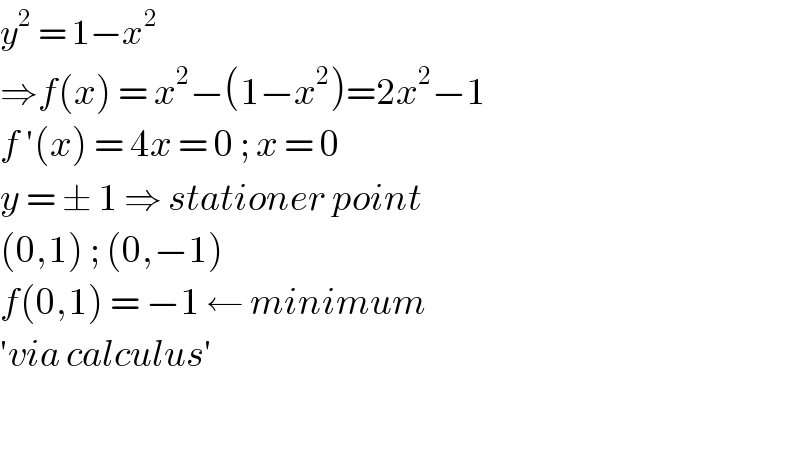
$${y}^{\mathrm{2}} \:=\:\mathrm{1}−{x}^{\mathrm{2}} \\ $$$$\Rightarrow{f}\left({x}\right)\:=\:{x}^{\mathrm{2}} −\left(\mathrm{1}−{x}^{\mathrm{2}} \right)=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1} \\ $$$${f}\:'\left({x}\right)\:=\:\mathrm{4}{x}\:=\:\mathrm{0}\:;\:{x}\:=\:\mathrm{0} \\ $$$${y}\:=\:\pm\:\mathrm{1}\:\Rightarrow\:{stationer}\:{point} \\ $$$$\left(\mathrm{0},\mathrm{1}\right)\:;\:\left(\mathrm{0},−\mathrm{1}\right)\: \\ $$$${f}\left(\mathrm{0},\mathrm{1}\right)\:=\:−\mathrm{1}\:\leftarrow\:{minimum}\: \\ $$$$'{via}\:{calculus}' \\ $$$$ \\ $$
Commented by mr W last updated on 19/Apr/20
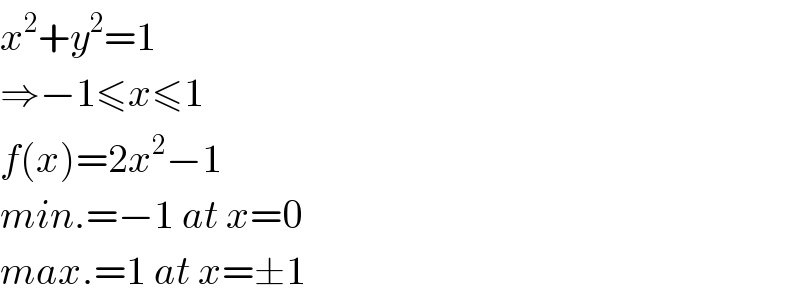
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow−\mathrm{1}\leqslant{x}\leqslant\mathrm{1} \\ $$$${f}\left({x}\right)=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1} \\ $$$${min}.=−\mathrm{1}\:{at}\:{x}=\mathrm{0} \\ $$$${max}.=\mathrm{1}\:{at}\:{x}=\pm\mathrm{1} \\ $$
Commented by jagoll last updated on 19/Apr/20
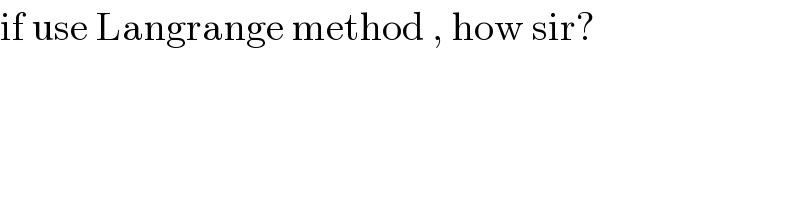
$$\mathrm{if}\:\mathrm{use}\:\mathrm{Langrange}\:\mathrm{method}\:,\:\mathrm{how}\:\mathrm{sir}? \\ $$
Answered by mr W last updated on 19/Apr/20
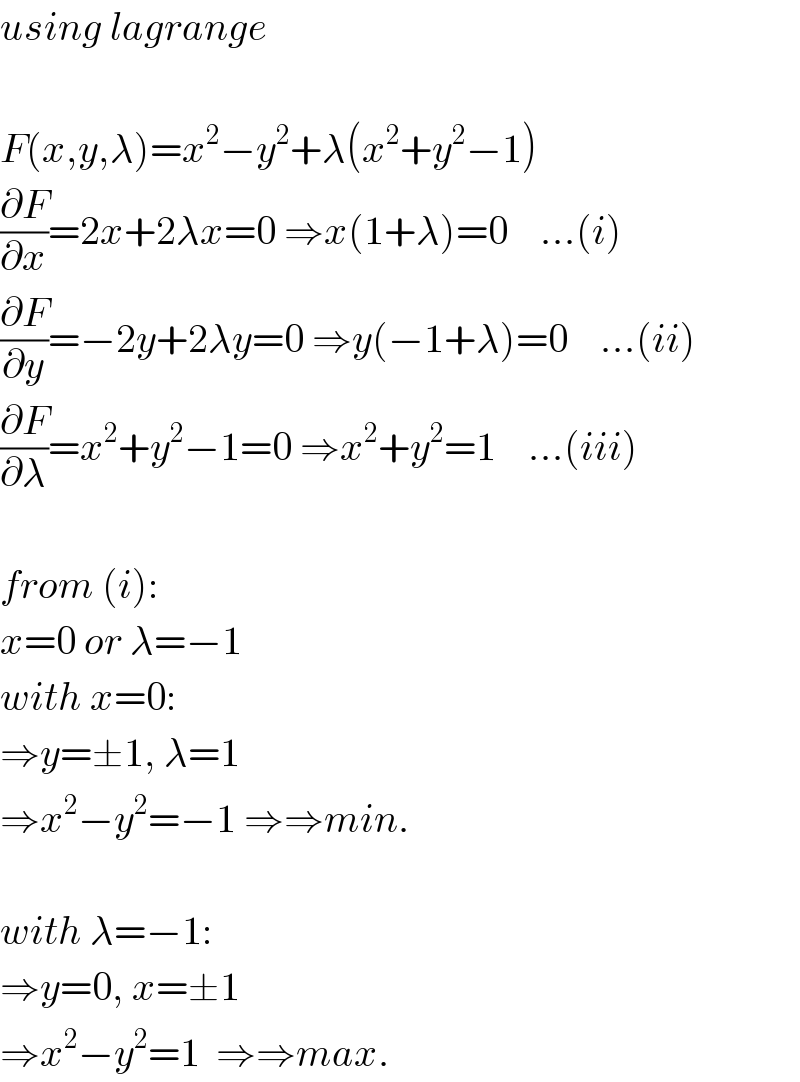
$${using}\:{lagrange} \\ $$$$ \\ $$$${F}\left({x},{y},\lambda\right)={x}^{\mathrm{2}} −{y}^{\mathrm{2}} +\lambda\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\frac{\partial{F}}{\partial{x}}=\mathrm{2}{x}+\mathrm{2}\lambda{x}=\mathrm{0}\:\Rightarrow{x}\left(\mathrm{1}+\lambda\right)=\mathrm{0}\:\:\:\:…\left({i}\right) \\ $$$$\frac{\partial{F}}{\partial{y}}=−\mathrm{2}{y}+\mathrm{2}\lambda{y}=\mathrm{0}\:\Rightarrow{y}\left(−\mathrm{1}+\lambda\right)=\mathrm{0}\:\:\:\:…\left({ii}\right) \\ $$$$\frac{\partial{F}}{\partial\lambda}={x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\:\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}\:\:\:\:…\left({iii}\right) \\ $$$$ \\ $$$${from}\:\left({i}\right): \\ $$$${x}=\mathrm{0}\:{or}\:\lambda=−\mathrm{1} \\ $$$${with}\:{x}=\mathrm{0}: \\ $$$$\Rightarrow{y}=\pm\mathrm{1},\:\lambda=\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =−\mathrm{1}\:\Rightarrow\Rightarrow{min}. \\ $$$$ \\ $$$${with}\:\lambda=−\mathrm{1}: \\ $$$$\Rightarrow{y}=\mathrm{0},\:{x}=\pm\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{1}\:\:\Rightarrow\Rightarrow{max}. \\ $$
Commented by jagoll last updated on 19/Apr/20
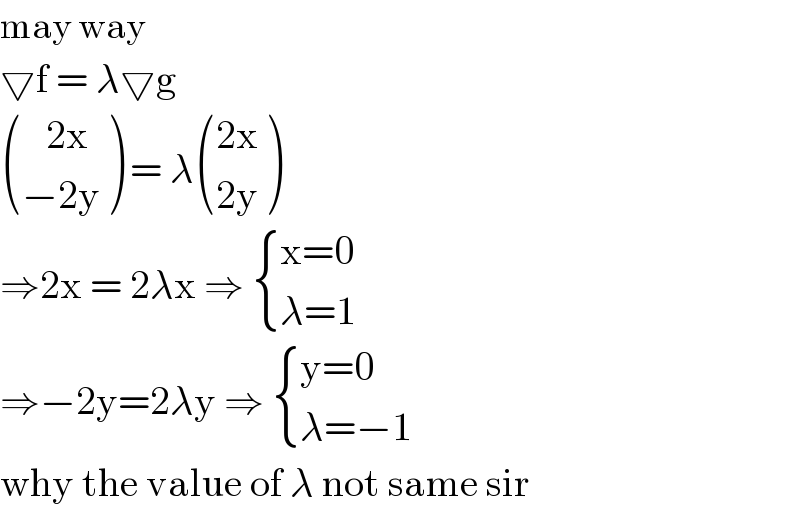
$$\mathrm{may}\:\mathrm{way}\: \\ $$$$\bigtriangledown\mathrm{f}\:=\:\lambda\bigtriangledown\mathrm{g} \\ $$$$\begin{pmatrix}{\:\:\:\mathrm{2x}}\\{−\mathrm{2y}}\end{pmatrix}\:=\:\lambda\begin{pmatrix}{\mathrm{2x}}\\{\mathrm{2y}}\end{pmatrix} \\ $$$$\Rightarrow\mathrm{2x}\:=\:\mathrm{2}\lambda\mathrm{x}\:\Rightarrow\:\begin{cases}{\mathrm{x}=\mathrm{0}}\\{\lambda=\mathrm{1}}\end{cases} \\ $$$$\Rightarrow−\mathrm{2y}=\mathrm{2}\lambda\mathrm{y}\:\Rightarrow\:\begin{cases}{\mathrm{y}=\mathrm{0}}\\{\lambda=−\mathrm{1}}\end{cases} \\ $$$$\mathrm{why}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\lambda\:\mathrm{not}\:\mathrm{same}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 19/Apr/20
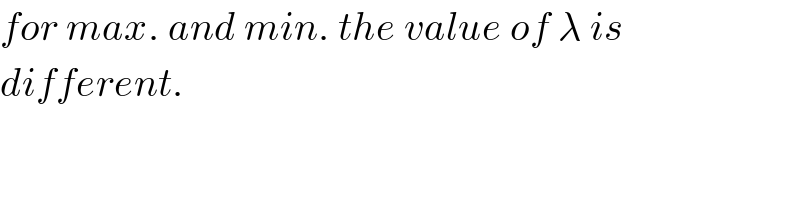
$${for}\:{max}.\:{and}\:{min}.\:{the}\:{value}\:{of}\:\lambda\:{is} \\ $$$${different}. \\ $$
Commented by mr W last updated on 19/Apr/20
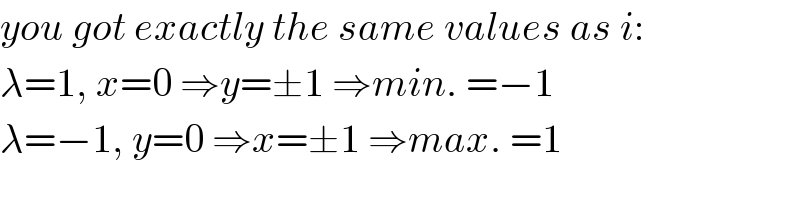
$${you}\:{got}\:{exactly}\:{the}\:{same}\:{values}\:{as}\:{i}: \\ $$$$\lambda=\mathrm{1},\:{x}=\mathrm{0}\:\Rightarrow{y}=\pm\mathrm{1}\:\Rightarrow{min}.\:=−\mathrm{1} \\ $$$$\lambda=−\mathrm{1},\:{y}=\mathrm{0}\:\Rightarrow{x}=\pm\mathrm{1}\:\Rightarrow{max}.\:=\mathrm{1} \\ $$
Commented by jagoll last updated on 19/Apr/20
$$\mathrm{o}\:\mathrm{i}\:\mathrm{understand}\:\mathrm{sir}.\:\mathrm{thank}\:\mathrm{you} \\ $$
