Question Number 44526 by arnabmaiti550@gmail.com last updated on 30/Sep/18
$$\mathrm{Find}\:\mathrm{moment}\:\mathrm{of}\:\mathrm{inertia}\:\mathrm{of}\:\mathrm{the}\:\mathrm{area}\:\mathrm{bounded} \\ $$$$\mathrm{by}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{r}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} \mathrm{cos2}\theta \\ $$$$\mathrm{about}\:\mathrm{its}\:\mathrm{axis} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 01/Oct/18
Answered by ajfour last updated on 30/Sep/18
![I =∫_0 ^( 2π) [∫_0 ^( r) ρr^2 (rdr)]dθ = (ρ/4)∫_0 ^( 2π) a^4 cos^2 2θ dθ = ((ρa^4 )/8)∫_0 ^( 2π) (1+cos 4θ)dθ = ((𝛒a^4 𝛑)/4) .](https://www.tinkutara.com/question/Q44530.png)
$${I}\:=\int_{\mathrm{0}} ^{\:\:\mathrm{2}\pi} \left[\int_{\mathrm{0}} ^{\:\:{r}} \:\rho{r}^{\mathrm{2}} \left({rdr}\right)\right]{d}\theta \\ $$$$\:\:=\:\frac{\rho}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\:\mathrm{2}\pi} {a}^{\mathrm{4}} \mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\theta\:{d}\theta \\ $$$$\:\:=\:\frac{\rho{a}^{\mathrm{4}} }{\mathrm{8}}\int_{\mathrm{0}} ^{\:\:\mathrm{2}\pi} \left(\mathrm{1}+\mathrm{cos}\:\mathrm{4}\theta\right){d}\theta \\ $$$$\:\:\:=\:\frac{\boldsymbol{\rho{a}}^{\mathrm{4}} \boldsymbol{\pi}}{\mathrm{4}}\:. \\ $$
Commented by arnabmaiti550@gmail.com last updated on 01/Oct/18
$$\mathrm{please}\:\mathrm{explain}\:\mathrm{the}\:\mathrm{first}\:\mathrm{line} \\ $$
Commented by ajfour last updated on 01/Oct/18
$${I}=\int{r}^{\mathrm{2}} {dm}\:\:=\:\int{r}^{\mathrm{2}} \rho\left({dA}\right) \\ $$$${A}\:{is}\:{area},\:\rho\:{is}\:{mass}\:{per}\:{unit}\:{area}. \\ $$$${I}=\int_{\mathrm{0}} ^{\:\:\mathrm{2}\pi} \rho{r}^{\mathrm{2}} \left({rdr}\right){d}\theta\:. \\ $$
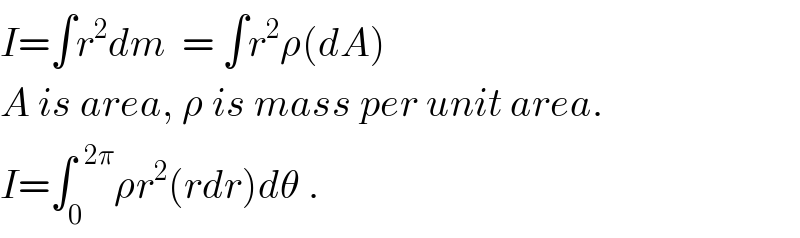
Commented by arnabmaiti550@gmail.com last updated on 01/Oct/18
$$\mathrm{Thank}\:\mathrm{u}\:\mathrm{sir}.\:\mathrm{Now}\:\mathrm{I}\:\mathrm{can}\:\mathrm{understand} \\ $$