Question Number 28814 by abdo imad last updated on 30/Jan/18
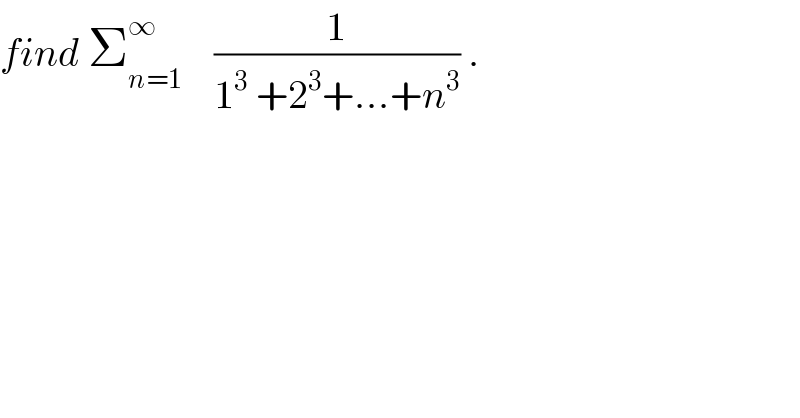
$${find}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{3}} \:+\mathrm{2}^{\mathrm{3}} +…+{n}^{\mathrm{3}} }\:. \\ $$
Commented by abdo imad last updated on 01/Feb/18
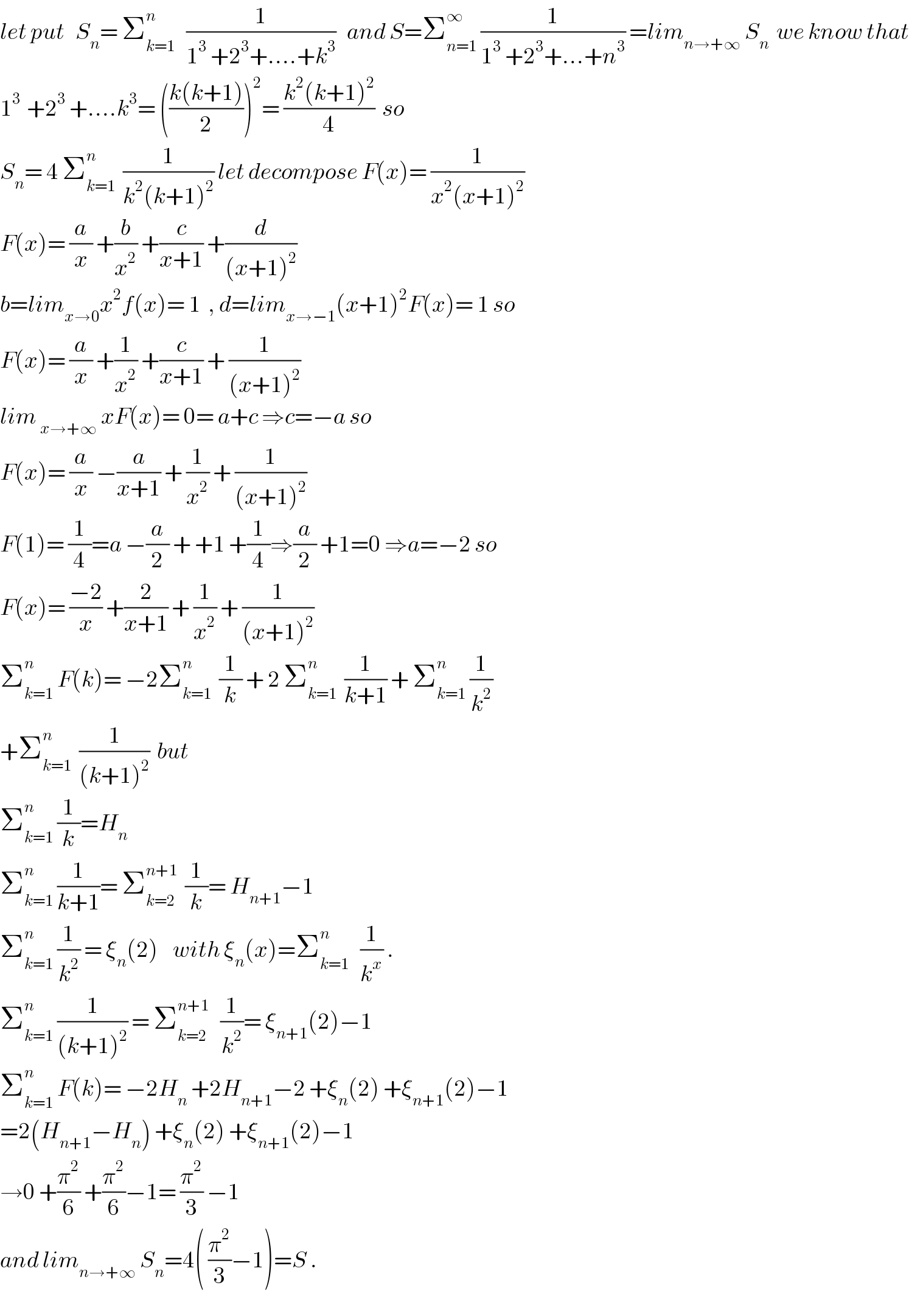
$${let}\:{put}\:\:\:{S}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{3}} \:+\mathrm{2}^{\mathrm{3}} +….+{k}^{\mathrm{3}} }\:\:\:{and}\:{S}=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{3}} \:+\mathrm{2}^{\mathrm{3}} +…+{n}^{\mathrm{3}} }\:={lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} \:\:{we}\:{know}\:{that} \\ $$$$\mathrm{1}^{\mathrm{3}\:} \:+\mathrm{2}^{\mathrm{3}} \:+….{k}^{\mathrm{3}} =\:\left(\frac{{k}\left({k}+\mathrm{1}\right)}{\mathrm{2}}\right)^{\mathrm{2}} =\:\frac{{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}\:\:{so} \\ $$$${S}_{{n}} =\:\mathrm{4}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} \left({k}+\mathrm{1}\right)^{\mathrm{2}} }\:{let}\:{decompose}\:{F}\left({x}\right)=\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${F}\left({x}\right)=\:\frac{{a}}{{x}}\:+\frac{{b}}{{x}^{\mathrm{2}} }\:+\frac{{c}}{{x}+\mathrm{1}}\:+\frac{{d}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${b}={lim}_{{x}\rightarrow\mathrm{0}} {x}^{\mathrm{2}} {f}\left({x}\right)=\:\mathrm{1}\:\:,\:{d}={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} {F}\left({x}\right)=\:\mathrm{1}\:{so} \\ $$$${F}\left({x}\right)=\:\frac{{a}}{{x}}\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\frac{{c}}{{x}+\mathrm{1}}\:+\:\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${lim}\:_{{x}\rightarrow+\infty} \:{xF}\left({x}\right)=\:\mathrm{0}=\:{a}+{c}\:\Rightarrow{c}=−{a}\:{so} \\ $$$${F}\left({x}\right)=\:\frac{{a}}{{x}}\:−\frac{{a}}{{x}+\mathrm{1}}\:+\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{1}\right)=\:\frac{\mathrm{1}}{\mathrm{4}}={a}\:−\frac{{a}}{\mathrm{2}}\:+\:+\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow\frac{{a}}{\mathrm{2}}\:+\mathrm{1}=\mathrm{0}\:\Rightarrow{a}=−\mathrm{2}\:{so} \\ $$$${F}\left({x}\right)=\:\frac{−\mathrm{2}}{{x}}\:+\frac{\mathrm{2}}{{x}+\mathrm{1}}\:+\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:{F}\left({k}\right)=\:−\mathrm{2}\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{{k}}\:+\:\mathrm{2}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{{k}+\mathrm{1}}\:+\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\: \\ $$$$+\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} }\:\:{but} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}={H}_{{n}} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{1}}=\:\sum_{{k}=\mathrm{2}} ^{{n}+\mathrm{1}} \:\:\frac{\mathrm{1}}{{k}}=\:{H}_{{n}+\mathrm{1}} −\mathrm{1}\:\: \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:=\:\xi_{{n}} \left(\mathrm{2}\right)\:\:\:\:{with}\:\xi_{{n}} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{\mathrm{1}}{{k}^{{x}} }\:. \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\sum_{{k}=\mathrm{2}} ^{{n}+\mathrm{1}} \:\:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }=\:\xi_{{n}+\mathrm{1}} \left(\mathrm{2}\right)−\mathrm{1} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:{F}\left({k}\right)=\:−\mathrm{2}{H}_{{n}} \:+\mathrm{2}{H}_{{n}+\mathrm{1}} −\mathrm{2}\:+\xi_{{n}} \left(\mathrm{2}\right)\:+\xi_{{n}+\mathrm{1}} \left(\mathrm{2}\right)−\mathrm{1} \\ $$$$=\mathrm{2}\left({H}_{{n}+\mathrm{1}} −{H}_{{n}} \right)\:+\xi_{{n}} \left(\mathrm{2}\right)\:+\xi_{{n}+\mathrm{1}} \left(\mathrm{2}\right)−\mathrm{1} \\ $$$$\rightarrow\mathrm{0}\:+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1}=\:\frac{\pi^{\mathrm{2}} }{\mathrm{3}}\:−\mathrm{1} \\ $$$${and}\:{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\mathrm{4}\left(\:\frac{\pi^{\mathrm{2}} }{\mathrm{3}}−\mathrm{1}\right)={S}\:. \\ $$
Commented by abdo imad last updated on 01/Feb/18
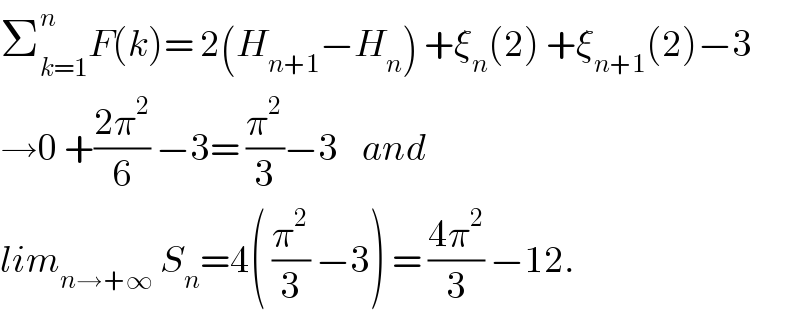
$$\sum_{{k}=\mathrm{1}} ^{{n}} {F}\left({k}\right)=\:\mathrm{2}\left({H}_{{n}+\mathrm{1}} −{H}_{{n}} \right)\:+\xi_{{n}} \left(\mathrm{2}\right)\:+\xi_{{n}+\mathrm{1}} \left(\mathrm{2}\right)−\mathrm{3} \\ $$$$\rightarrow\mathrm{0}\:+\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{6}}\:−\mathrm{3}=\:\frac{\pi^{\mathrm{2}} }{\mathrm{3}}−\mathrm{3}\:\:\:\:{and} \\ $$$${lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\mathrm{4}\left(\:\frac{\pi^{\mathrm{2}} }{\mathrm{3}}\:−\mathrm{3}\right)\:=\:\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{3}}\:−\mathrm{12}. \\ $$
