Menu Close

find-n-1-1-5-n-1-or-generally-k-n-1-1-k-n-1-with-k-N-k-2-

Tinku Tara 0 Comments
Pin




Question Number 162261 by mr W last updated on 28/Dec/21
find Σ_(n=1) ^∞ (1/(5^n −1))=? or generally Φ(k)= Σ_(n=1) ^∞ (1/(k^n −1))=? with k∈N, k≥2
$${find}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{5}^{{n}} −\mathrm{1}}=? \\ $$$${or}\:{generally} \\ $$$$\Phi\left({k}\right)=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{k}^{{n}} −\mathrm{1}}=?\:{with}\:{k}\in{N},\:{k}\geqslant\mathrm{2} \\ $$
Commented by mindispower last updated on 28/Dec/21
just completed why the[lther form
$${just}\:{completed}\:{why}\:\:{the}\left[{lther}\:{form}\right. \\ $$
Answered by aleks041103 last updated on 28/Dec/21
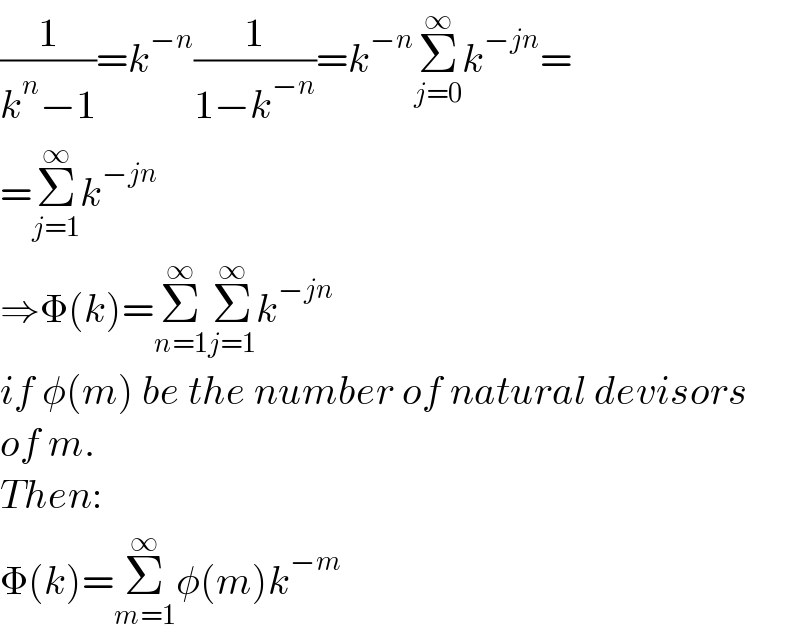
(1/(k^n −1))=k^(−n) (1/(1−k^(−n) ))=k^(−n) Σ_(j=0) ^∞ k^(−jn) = =Σ_(j=1) ^∞ k^(−jn) ⇒Φ(k)=Σ_(n=1) ^∞ Σ_(j=1) ^∞ k^(−jn) if φ(m) be the number of natural devisors of m. Then: Φ(k)=Σ_(m=1) ^∞ φ(m)k^(−m)
$$\frac{\mathrm{1}}{{k}^{{n}} −\mathrm{1}}={k}^{−{n}} \frac{\mathrm{1}}{\mathrm{1}−{k}^{−{n}} }={k}^{−{n}} \underset{{j}=\mathrm{0}} {\overset{\infty} {\sum}}{k}^{−{jn}} = \\ $$$$=\underset{{j}=\mathrm{1}} {\overset{\infty} {\sum}}{k}^{−{jn}} \\ $$$$\Rightarrow\Phi\left({k}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{j}=\mathrm{1}} {\overset{\infty} {\sum}}{k}^{−{jn}} \\ $$$${if}\:\phi\left({m}\right)\:{be}\:{the}\:{number}\:{of}\:{natural}\:{devisors} \\ $$$${of}\:{m}. \\ $$$${Then}: \\ $$$$\Phi\left({k}\right)=\underset{{m}=\mathrm{1}} {\overset{\infty} {\sum}}\phi\left({m}\right){k}^{−{m}} \\ $$
Commented by aleks041103 last updated on 28/Dec/21
to be continued
$${to}\:{be}\:{continued} \\ $$
Answered by aleks041103 last updated on 28/Dec/21
The q−digama function ψ_q (z) is ψ_q (z)=(1/(Γ_q (z))) ((∂Γ_q (z))/∂z) where Γ_q (z) is the q−gamma function Γ_q (z)=(1−q)^(1−z) Π_(n=0) ^∞ ((1−q^(n+1) )/(1−q^(n+z) )) another form of q−digamma is ψ_q (z)=−ln(1−q) + ln(q)Σ_(n=0) ^∞ (q^(n+z) /(1−q^(n+z) )) ⇒ψ_q (1)=−ln(1−q) + ln(q)Σ_(n=0) ^∞ (q^(n+1) /(1−q^(n+1) )) But Σ_(n=0) ^∞ (q^(n+1) /(1−q^(n+1) ))=Σ_(n=1) ^∞ (1/(q^(−n) −1))=Σ_(n=0) ^∞ (1/(((1/q))^n −1))=Φ((1/q)) ⇒ψ_q (1)=−ln(1−q) + ln(q)Φ(1/q) ⇒Φ(1/q)=((ψ_q (1)+ln(1−q))/(ln(q))) ⇒Φ(k)=((ψ_(1/k) (1)+ln(1−1/k))/(ln(1/k)))= =((ln((k/(k−1)))−ψ_(1/k) (1))/(ln(k))) ⇒Φ(k)=Σ_(n=1) ^∞ (1/(k^n −1))=((ln((k/(k−1)))−ψ_(1/k) (1))/(ln(k)))
$${The}\:{q}−{digama}\:{function}\:\psi_{{q}} \left({z}\right)\:{is} \\ $$$$\psi_{{q}} \left({z}\right)=\frac{\mathrm{1}}{\Gamma_{{q}} \left({z}\right)}\:\frac{\partial\Gamma_{{q}} \left({z}\right)}{\partial{z}} \\ $$$${where}\:\Gamma_{{q}} \left({z}\right)\:{is}\:{the}\:{q}−{gamma}\:{function} \\ $$$$\Gamma_{{q}} \left({z}\right)=\left(\mathrm{1}−{q}\right)^{\mathrm{1}−{z}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\prod}}\frac{\mathrm{1}−{q}^{{n}+\mathrm{1}} }{\mathrm{1}−{q}^{{n}+{z}} } \\ $$$${another}\:{form}\:{of}\:{q}−{digamma}\:{is} \\ $$$$\psi_{{q}} \left({z}\right)=−{ln}\left(\mathrm{1}−{q}\right)\:+\:{ln}\left({q}\right)\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{q}^{{n}+{z}} }{\mathrm{1}−{q}^{{n}+{z}} } \\ $$$$\Rightarrow\psi_{{q}} \left(\mathrm{1}\right)=−{ln}\left(\mathrm{1}−{q}\right)\:+\:{ln}\left({q}\right)\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{q}^{{n}+\mathrm{1}} }{\mathrm{1}−{q}^{{n}+\mathrm{1}} } \\ $$$${But} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{q}^{{n}+\mathrm{1}} }{\mathrm{1}−{q}^{{n}+\mathrm{1}} }=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{q}^{−{n}} −\mathrm{1}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{{q}}\right)^{{n}} −\mathrm{1}}=\Phi\left(\frac{\mathrm{1}}{{q}}\right) \\ $$$$\Rightarrow\psi_{{q}} \left(\mathrm{1}\right)=−{ln}\left(\mathrm{1}−{q}\right)\:+\:{ln}\left({q}\right)\Phi\left(\mathrm{1}/{q}\right) \\ $$$$\Rightarrow\Phi\left(\mathrm{1}/{q}\right)=\frac{\psi_{{q}} \left(\mathrm{1}\right)+{ln}\left(\mathrm{1}−{q}\right)}{{ln}\left({q}\right)} \\ $$$$\Rightarrow\Phi\left({k}\right)=\frac{\psi_{\mathrm{1}/{k}} \left(\mathrm{1}\right)+{ln}\left(\mathrm{1}−\mathrm{1}/{k}\right)}{{ln}\left(\mathrm{1}/{k}\right)}= \\ $$$$=\frac{{ln}\left(\frac{{k}}{{k}−\mathrm{1}}\right)−\psi_{\mathrm{1}/{k}} \left(\mathrm{1}\right)}{{ln}\left({k}\right)} \\ $$$$\Rightarrow\Phi\left({k}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{{n}} −\mathrm{1}}=\frac{{ln}\left(\frac{{k}}{{k}−\mathrm{1}}\right)−\psi_{\mathrm{1}/{k}} \left(\mathrm{1}\right)}{{ln}\left({k}\right)} \\ $$
Commented by mr W last updated on 28/Dec/21
thanks alot sir!
$${thanks}\:{alot}\:{sir}! \\ $$
Commented by Tawa11 last updated on 28/Dec/21
Weldone sir
$$\mathrm{Weldone}\:\mathrm{sir} \\ $$
Commented by mindispower last updated on 28/Dec/21
nice sir
$${nice}\:{sir} \\ $$
Answered by mindispower last updated on 28/Dec/21
starting Withe q−Gamma function{function we found in q series expension mldular arithmetics ” famous using Ramanujan Γ_q (z)=(1−q)^(1−z) (((q;q)_∞ )/((q^z ;q)_∞ ))=(1−q)^(x−1) Π_(n≥0) (((1−q^(n+1) ))/((1−q^(n+z) ))) Ψ_q (z)=(1/(Γ_q (z))).((dΓ_q (z))/dz) q−digamma function =(1/(Γ_q (z))).(d/dz)((1−q)^(1−z) Π_(n≥0) (((1−q^(n+1) ))/((1−q^(n+z) )))) =(1/(Γ_q (z))).(−ln(1−q).(1−q)^(z−1) .Π_(n≥0) (((1−q^(n+1) )/(1−q^(n+z) ))+(1−q)^(1−z) .Σ_(j≥0) (((1−q^(j+1) )ln(q)q^(j+z) )/((1−q^(j+z) )^2 ))Π_(n≥0,n≠j) (((1−q)^(n+1) )/((1−q^(n+z) ))) =(1/(Γ_q (z)))[ln(1−q).Γ_q (z)+Σ_(j≥0) .(((1−q^(j+1) )ln(q)q^(j+z) )/((1−q^(j+z) )^2 )).((Γ_q (z)(1−q^(j+z) ))/((1−q^j )))] Ψ_q (z)=−ln(1−q)+ln(q)Σ_(j≥0) (q^(j+z) /(1−q^(j+z) ))......(E) S=Σ_(n≥1) (1/(5^n −1))=Σ_(n≥1) ((((1/5))^n )/(1−((1/5))^n )) (E)⇔ϖ_q (z)Σ_(j≥0) (q^(j+z) /(1−q^(j+z) ))=((Ψ_q (z)+ln(1−q))/(ln(q))) ϖ_(1/5) (1)=Σ_(n≥0) ((((1/5))^(n+1) )/(1−((1/5))^(n+1) ))=S=((Ψ_(((1/5))) (1)+ln((4/5)))/(−ln(5))) ϖ_(1/k) (1)=Φ(k)=Σ_(n≥1) (1/(k^n −1))=((Ψ_(1/k) (1)+ln(((k−1)/k)))/(−ln(k)))
$${starting}\:{Withe}\:{q}−{Gamma}\:{function}\left\{{function}\:{we}\:{found}\right. \\ $$$${in}\:{q}\:{series}\:{expension}\:{mldular}\:{arithmetics}\:'' \\ $$$${famous}\:{using}\:{Ramanujan} \\ $$$$\Gamma_{{q}} \left({z}\right)=\left(\mathrm{1}−{q}\right)^{\mathrm{1}−{z}} \frac{\left(\boldsymbol{{q}};{q}\right)_{\infty} }{\left({q}^{{z}} ;{q}\right)_{\infty} }=\left(\mathrm{1}−{q}\right)^{{x}−\mathrm{1}} \underset{{n}\geqslant\mathrm{0}} {\prod}\frac{\left(\mathrm{1}−{q}^{{n}+\mathrm{1}} \right)}{\left(\mathrm{1}−{q}^{{n}+{z}} \right)} \\ $$$$\Psi_{{q}} \left({z}\right)=\frac{\mathrm{1}}{\Gamma_{{q}} \left({z}\right)}.\frac{{d}\Gamma_{{q}} \left({z}\right)}{{dz}}\:\:\:\:\:{q}−{digamma}\:{function} \\ $$$$=\frac{\mathrm{1}}{\Gamma_{{q}} \left({z}\right)}.\frac{{d}}{{dz}}\left(\left(\mathrm{1}−{q}\right)^{\mathrm{1}−{z}} \underset{{n}\geqslant\mathrm{0}} {\prod}\frac{\left(\mathrm{1}−{q}^{{n}+\mathrm{1}} \right)}{\left(\mathrm{1}−{q}^{{n}+{z}} \right)}\right) \\ $$$$ \\ $$$$=\frac{\mathrm{1}}{\Gamma_{{q}} \left({z}\right)}.\left(−{ln}\left(\mathrm{1}−{q}\right).\left(\mathrm{1}−{q}\right)^{{z}−\mathrm{1}} .\underset{{n}\geqslant\mathrm{0}} {\prod}\frac{\left(\mathrm{1}−{q}^{{n}+\mathrm{1}} \right.}{\mathrm{1}−{q}^{{n}+{z}} }+\left(\mathrm{1}−{q}\right)^{\mathrm{1}−{z}} .\underset{{j}\geqslant\mathrm{0}} {\sum}\frac{\left(\mathrm{1}−{q}^{{j}+\mathrm{1}} \right){ln}\left({q}\right){q}^{{j}+{z}} }{\left(\mathrm{1}−{q}^{{j}+{z}} \right)^{\mathrm{2}} }\underset{{n}\geqslant\mathrm{0},{n}\neq{j}} {\prod}\frac{\left(\mathrm{1}−{q}\right)^{{n}+\mathrm{1}} }{\left(\mathrm{1}−{q}^{{n}+{z}} \right)}\right. \\ $$$$=\frac{\mathrm{1}}{\Gamma_{{q}} \left({z}\right)}\left[{ln}\left(\mathrm{1}−{q}\right).\Gamma_{{q}} \left({z}\right)+\underset{{j}\geqslant\mathrm{0}} {\sum}.\frac{\left(\mathrm{1}−{q}^{{j}+\mathrm{1}} \right){ln}\left({q}\right){q}^{{j}+{z}} }{\left(\mathrm{1}−{q}^{{j}+{z}} \right)^{\mathrm{2}} }.\frac{\Gamma_{{q}} \left({z}\right)\left(\mathrm{1}−{q}^{{j}+{z}} \right)}{\left(\mathrm{1}−{q}^{{j}} \right)}\right] \\ $$$$\Psi_{{q}} \left({z}\right)=−{ln}\left(\mathrm{1}−{q}\right)+{ln}\left({q}\right)\underset{{j}\geqslant\mathrm{0}} {\sum}\frac{{q}^{{j}+{z}} }{\mathrm{1}−{q}^{{j}+{z}} }……\left({E}\right) \\ $$$${S}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\mathrm{5}^{{n}} −\mathrm{1}}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{{n}} }{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{{n}} } \\ $$$$\left({E}\right)\Leftrightarrow\varpi_{{q}} \left({z}\right)\underset{{j}\geqslant\mathrm{0}} {\sum}\frac{{q}^{{j}+{z}} }{\mathrm{1}−{q}^{{j}+{z}} }=\frac{\Psi_{{q}} \left({z}\right)+{ln}\left(\mathrm{1}−{q}\right)}{{ln}\left({q}\right)} \\ $$$$\varpi_{\frac{\mathrm{1}}{\mathrm{5}}} \left(\mathrm{1}\right)=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{{n}+\mathrm{1}} }{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{{n}+\mathrm{1}} }={S}=\frac{\Psi_{\left(\frac{\mathrm{1}}{\mathrm{5}}\right)} \left(\mathrm{1}\right)+{ln}\left(\frac{\mathrm{4}}{\mathrm{5}}\right)}{−{ln}\left(\mathrm{5}\right)} \\ $$$$\varpi_{\frac{\mathrm{1}}{{k}}} \left(\mathrm{1}\right)=\Phi\left({k}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{k}^{{n}} −\mathrm{1}}=\frac{\Psi_{\frac{\mathrm{1}}{{k}}} \left(\mathrm{1}\right)+{ln}\left(\frac{{k}−\mathrm{1}}{{k}}\right)}{−{ln}\left({k}\right)} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 28/Dec/21
thanks to you too sir!
$${thanks}\:{to}\:{you}\:{too}\:{sir}! \\ $$
Commented by mindispower last updated on 28/Dec/21
pleasur God bless you
$${pleasur}\:{God}\:{bless}\:{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *