Menu Close

find-n-1-1-n-n-1-2-n-1-

Tinku Tara 0 Comments
Pin




Question Number 33124 by prof Abdo imad last updated on 10/Apr/18
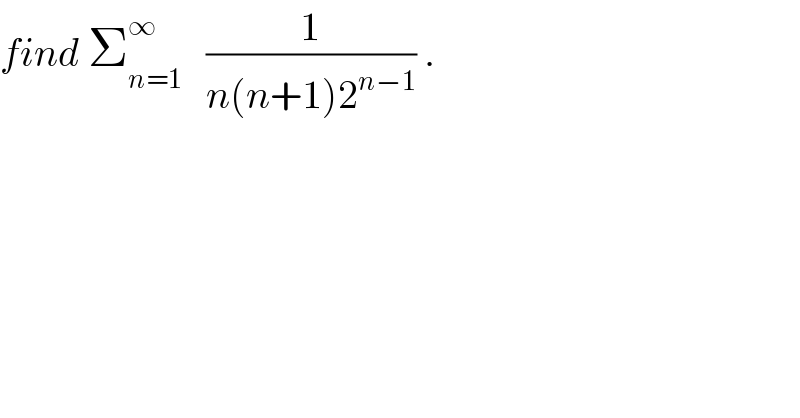
find Σ_(n=1) ^∞ (1/(n(n+1)2^(n−1) )) .
$${find}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\mathrm{2}^{{n}−\mathrm{1}} }\:. \\ $$
Commented by prof Abdo imad last updated on 15/Apr/18
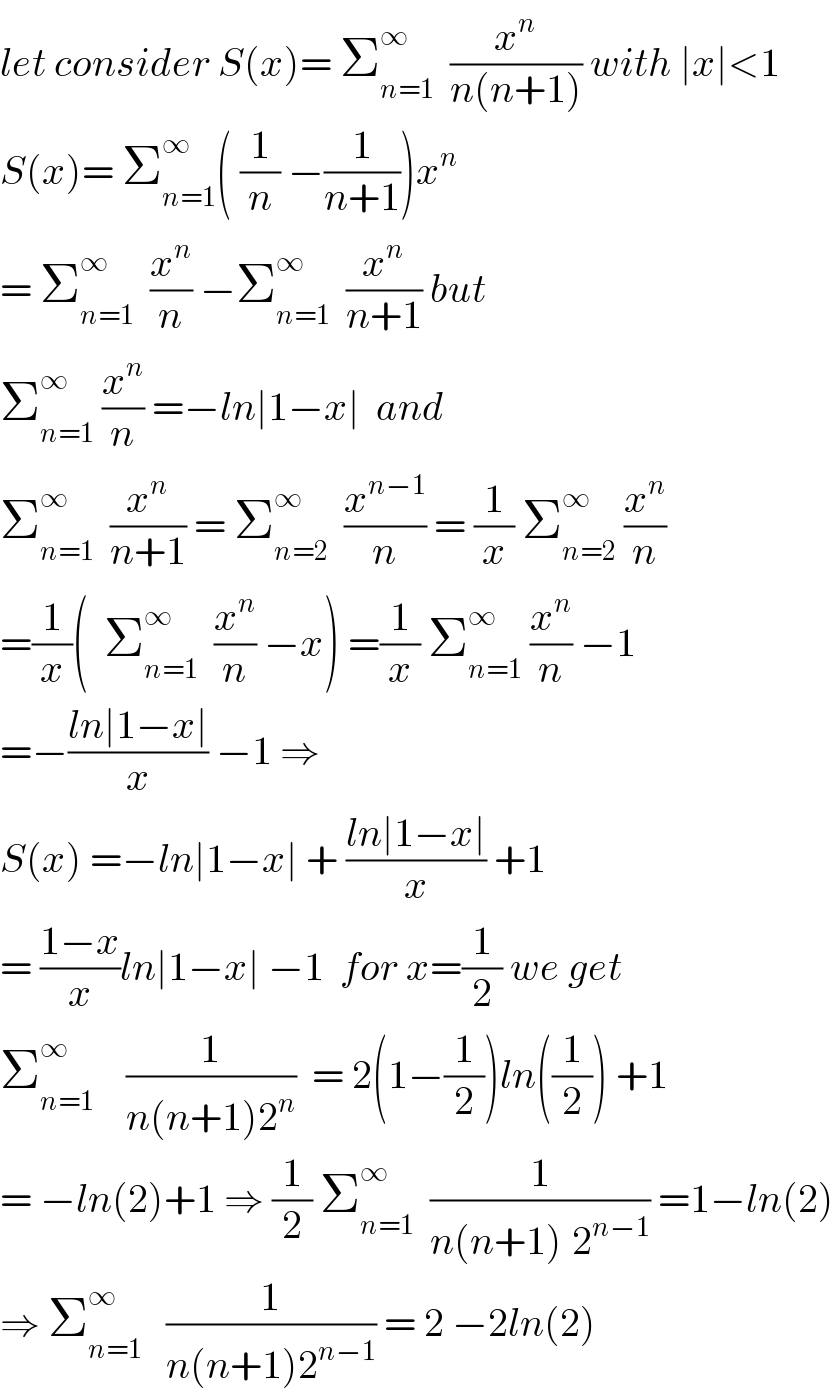
let consider S(x)= Σ_(n=1) ^∞ (x^n /(n(n+1))) with ∣x∣<1 S(x)= Σ_(n=1) ^∞ ( (1/n) −(1/(n+1)))x^n = Σ_(n=1) ^∞ (x^n /n) −Σ_(n=1) ^∞ (x^n /(n+1)) but Σ_(n=1) ^∞ (x^n /n) =−ln∣1−x∣ and Σ_(n=1) ^∞ (x^n /(n+1)) = Σ_(n=2) ^∞ (x^(n−1) /n) = (1/x) Σ_(n=2) ^∞ (x^n /n) =(1/x)( Σ_(n=1) ^∞ (x^n /n) −x) =(1/x) Σ_(n=1) ^∞ (x^n /n) −1 =−((ln∣1−x∣)/x) −1 ⇒ S(x) =−ln∣1−x∣ + ((ln∣1−x∣)/x) +1 = ((1−x)/x)ln∣1−x∣ −1 for x=(1/2) we get Σ_(n=1) ^∞ (1/(n(n+1)2^n )) = 2(1−(1/2))ln((1/2)) +1 = −ln(2)+1 ⇒ (1/2) Σ_(n=1) ^∞ (1/(n(n+1)^ 2^(n−1) )) =1−ln(2) ⇒ Σ_(n=1) ^∞ (1/(n(n+1)2^(n−1) )) = 2 −2ln(2)
$${let}\:{consider}\:{S}\left({x}\right)=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{x}^{{n}} }{{n}\left({n}+\mathrm{1}\right)}\:{with}\:\mid{x}\mid<\mathrm{1} \\ $$$${S}\left({x}\right)=\:\sum_{{n}=\mathrm{1}} ^{\infty} \left(\:\frac{\mathrm{1}}{{n}}\:−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right){x}^{{n}} \: \\ $$$$=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{x}^{{n}} }{{n}}\:−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{x}^{{n}} }{{n}+\mathrm{1}}\:{but}\: \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}\:=−{ln}\mid\mathrm{1}−{x}\mid\:\:{and} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{x}^{{n}} }{{n}+\mathrm{1}}\:=\:\sum_{{n}=\mathrm{2}} ^{\infty} \:\:\frac{{x}^{{n}−\mathrm{1}} }{{n}}\:=\:\frac{\mathrm{1}}{{x}}\:\sum_{{n}=\mathrm{2}} ^{\infty} \:\frac{{x}^{{n}} }{{n}} \\ $$$$=\frac{\mathrm{1}}{{x}}\left(\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{x}^{{n}} }{{n}}\:−{x}\right)\:=\frac{\mathrm{1}}{{x}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{x}^{{n}} }{{n}}\:−\mathrm{1} \\ $$$$=−\frac{{ln}\mid\mathrm{1}−{x}\mid}{{x}}\:−\mathrm{1}\:\Rightarrow \\ $$$${S}\left({x}\right)\:=−{ln}\mid\mathrm{1}−{x}\mid\:+\:\frac{{ln}\mid\mathrm{1}−{x}\mid}{{x}}\:+\mathrm{1} \\ $$$$=\:\frac{\mathrm{1}−{x}}{{x}}{ln}\mid\mathrm{1}−{x}\mid\:−\mathrm{1}\:\:{for}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\:{we}\:{get} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\mathrm{2}^{{n}} }\:\:=\:\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right){ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:+\mathrm{1}\: \\ $$$$=\:−{ln}\left(\mathrm{2}\right)+\mathrm{1}\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)^{} \mathrm{2}^{{n}−\mathrm{1}} }\:=\mathrm{1}−{ln}\left(\mathrm{2}\right) \\ $$$$\Rightarrow\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\mathrm{2}^{{n}−\mathrm{1}} }\:=\:\mathrm{2}\:−\mathrm{2}{ln}\left(\mathrm{2}\right)\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *