Question Number 38108 by maxmathsup by imad last updated on 21/Jun/18
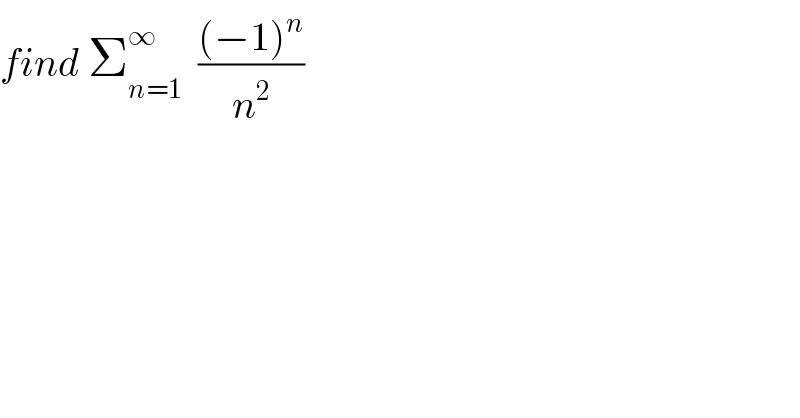
$${find}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} } \\ $$
Commented by prof Abdo imad last updated on 24/Jun/18
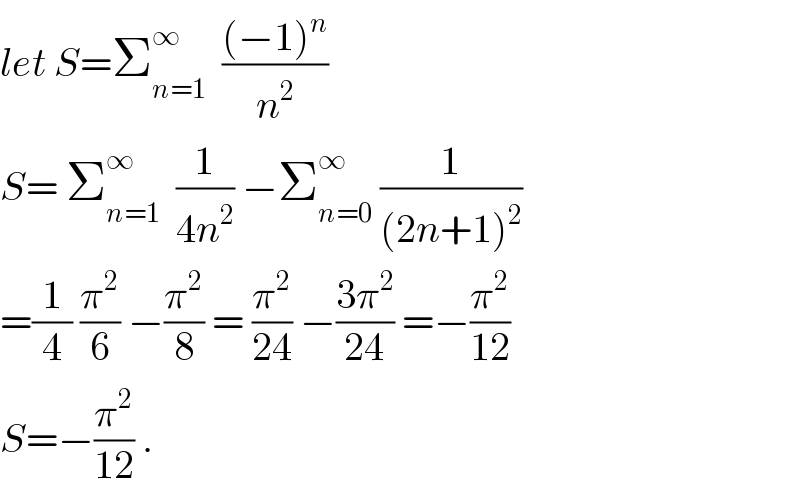
$${let}\:{S}=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} } \\ $$$${S}=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }\:−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{24}}\:−\frac{\mathrm{3}\pi^{\mathrm{2}} }{\mathrm{24}}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$${S}=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:. \\ $$
