Menu Close

find-n-1-1-n-n-cos-nx-and-n-1-1-n-n-sin-nx-

Tinku Tara 0 Comments
Pin




Question Number 38942 by math khazana by abdo last updated on 01/Jul/18
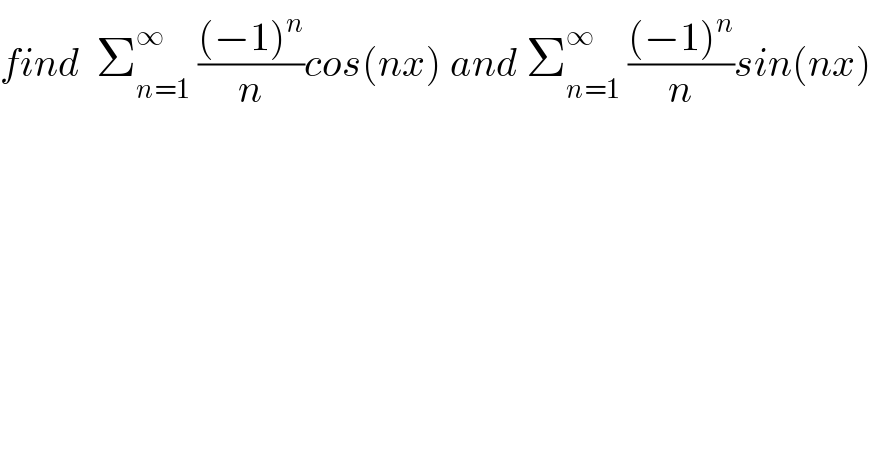
find Σ_(n=1) ^∞ (((−1)^n )/n)cos(nx) and Σ_(n=1) ^∞ (((−1)^n )/n)sin(nx)
find∑n=1∞(−1)nncos(nx)and∑n=1∞(−1)nnsin(nx)
Commented by prof Abdo imad last updated on 09/Jul/18
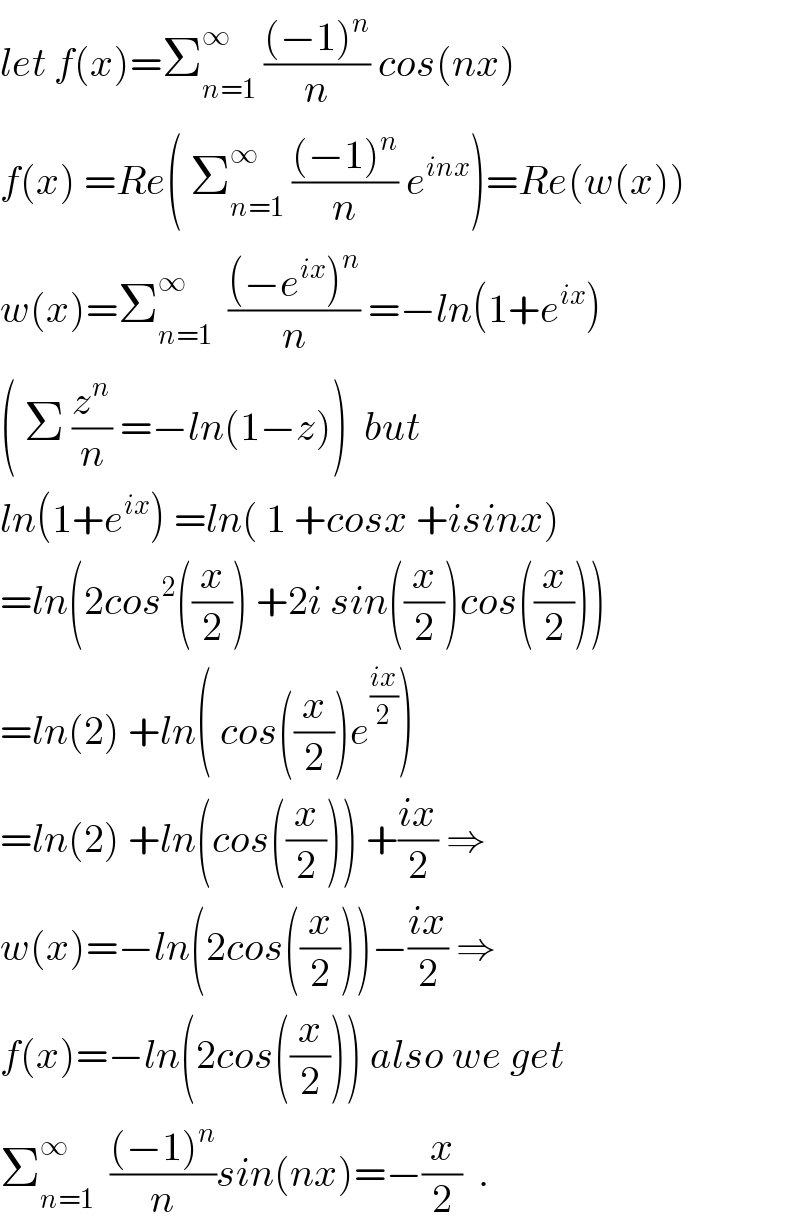
let f(x)=Σ_(n=1) ^∞ (((−1)^n )/n) cos(nx) f(x) =Re( Σ_(n=1) ^∞ (((−1)^n )/n) e^(inx) )=Re(w(x)) w(x)=Σ_(n=1) ^∞ (((−e^(ix) )^n )/n) =−ln(1+e^(ix) ) ( Σ (z^n /n) =−ln(1−z)) but ln(1+e^(ix) ) =ln( 1 +cosx +isinx) =ln(2cos^2 ((x/2)) +2i sin((x/2))cos((x/2))) =ln(2) +ln( cos((x/2))e^((ix)/2) ) =ln(2) +ln(cos((x/2))) +((ix)/2) ⇒ w(x)=−ln(2cos((x/2)))−((ix)/2) ⇒ f(x)=−ln(2cos((x/2))) also we get Σ_(n=1) ^∞ (((−1)^n )/n)sin(nx)=−(x/2) .
letf(x)=∑n=1∞(−1)nncos(nx)f(x)=Re(∑n=1∞(−1)nneinx)=Re(w(x))w(x)=∑n=1∞(−eix)nn=−ln(1+eix)(Σznn=−ln(1−z))butln(1+eix)=ln(1+cosx+isinx)=ln(2cos2(x2)+2isin(x2)cos(x2))=ln(2)+ln(cos(x2)eix2)=ln(2)+ln(cos(x2))+ix2⇒w(x)=−ln(2cos(x2))−ix2⇒f(x)=−ln(2cos(x2))alsoweget∑n=1∞(−1)nnsin(nx)=−x2.

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *