Menu Close

find-n-1-4n-2n-1-2-2n-1-2-

Tinku Tara 0 Comments
Pin




Question Number 38323 by math khazana by abdo last updated on 24/Jun/18
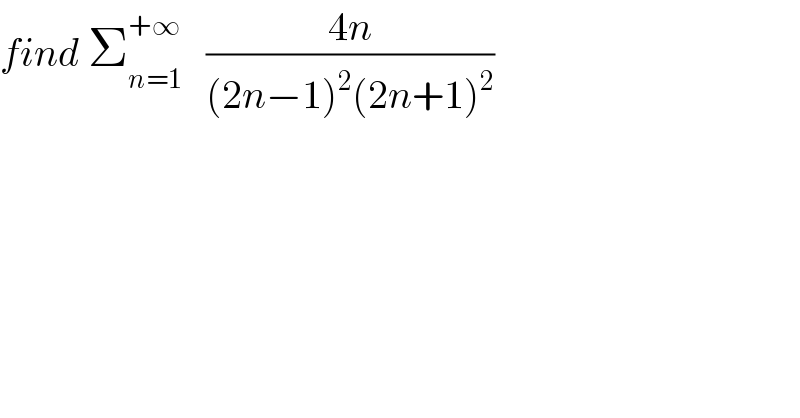
find Σ_(n=1) ^(+∞) ((4n)/((2n−1)^2 (2n+1)^2 ))
$${find}\:\sum_{{n}=\mathrm{1}} ^{+\infty} \:\:\:\frac{\mathrm{4}{n}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Commented by math khazana by abdo last updated on 25/Jun/18
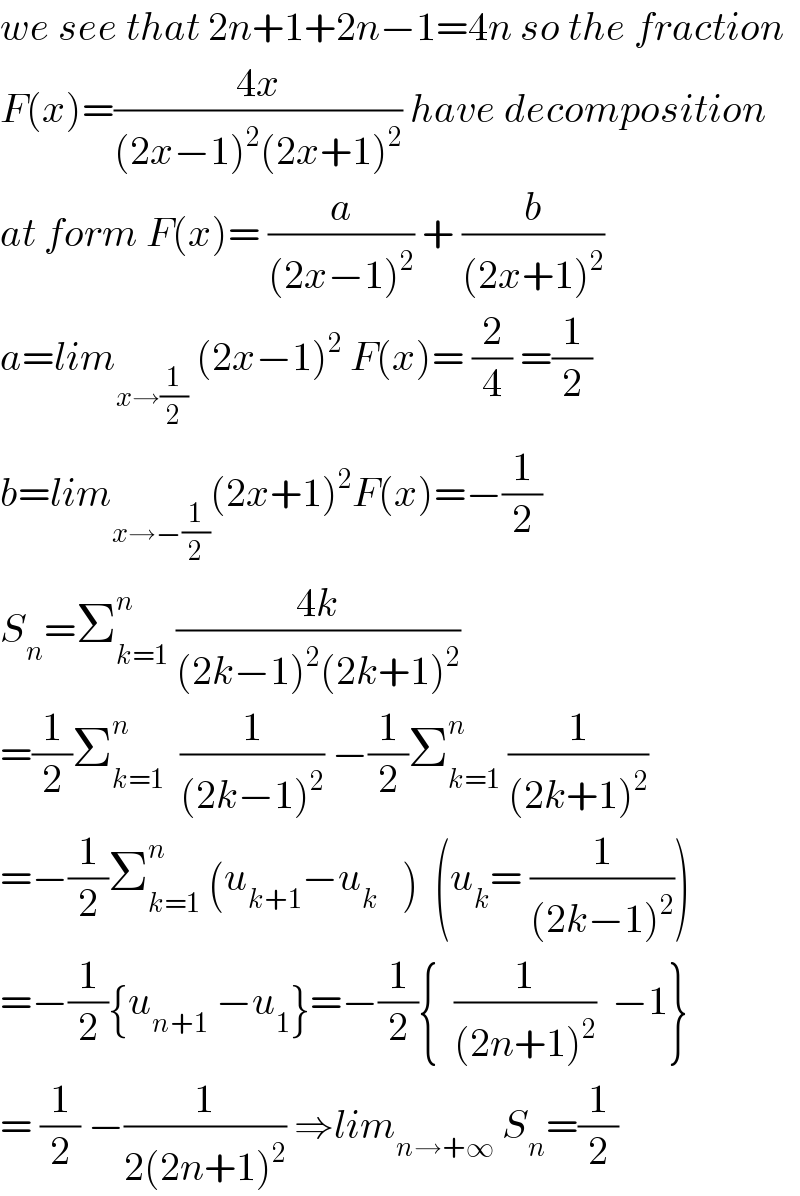
we see that 2n+1+2n−1=4n so the fraction F(x)=((4x)/((2x−1)^2 (2x+1)^2 )) have decomposition at form F(x)= (a/((2x−1)^2 )) + (b/((2x+1)^2 )) a=lim_(x→(1/2)) (2x−1)^2 F(x)= (2/4) =(1/2) b=lim_(x→−(1/2)) (2x+1)^2 F(x)=−(1/2) S_n =Σ_(k=1) ^n ((4k)/((2k−1)^2 (2k+1)^2 )) =(1/2)Σ_(k=1) ^n (1/((2k−1)^2 )) −(1/2)Σ_(k=1) ^n (1/((2k+1)^2 )) =−(1/2)Σ_(k=1) ^n (u_(k+1) −u_k ) (u_k = (1/((2k−1)^2 ))) =−(1/2){u_(n+1) −u_1 }=−(1/2){ (1/((2n+1)^2 )) −1} = (1/2) −(1/(2(2n+1)^2 )) ⇒lim_(n→+∞) S_n =(1/2)
$${we}\:{see}\:{that}\:\mathrm{2}{n}+\mathrm{1}+\mathrm{2}{n}−\mathrm{1}=\mathrm{4}{n}\:{so}\:{the}\:{fraction} \\ $$$${F}\left({x}\right)=\frac{\mathrm{4}{x}}{\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }\:{have}\:{decomposition} \\ $$$${at}\:{form}\:{F}\left({x}\right)=\:\frac{{a}}{\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} }\:+\:\frac{{b}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${a}={lim}_{{x}\rightarrow\frac{\mathrm{1}}{\mathrm{2}}} \:\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} \:{F}\left({x}\right)=\:\frac{\mathrm{2}}{\mathrm{4}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${b}={lim}_{{x}\rightarrow−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} {F}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{4}{k}}{\left(\mathrm{2}{k}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{k}−\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{1}} ^{{n}} \:\left({u}_{{k}+\mathrm{1}} −{u}_{{k}} \:\:\:\right)\:\:\left({u}_{{k}} =\:\frac{\mathrm{1}}{\left(\mathrm{2}{k}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left\{{u}_{{n}+\mathrm{1}} \:−{u}_{\mathrm{1}} \right\}=−\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\:−\mathrm{1}\right\} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/Jun/18
=(1/2){Σ_(n=1) ^(+∞) (1/((2n−1)^2 ))−(1/((2n+1)^2 ))} (1/2){((1/1^2 )+(1/3^2 )+(1/5^2 )+....)−((1/3^2 )+(1/5^2 )+(1/7^2 )+...)} =(1/2) i made a?mistake... (2n+1)^2 −(2n−1)^2 =4×2n×1=8n but in problem ((4n)/((2n+1)^2 (2n−1)^2 )) so(1/2){(1/((2n−1)^2 ))−(1/((2n+1)^2 ))} so (1/2) factor should be there... or methld 2s=(1/1^2 )−(1/3^2 ) +(1/3^2 )−(1/5^2 ) .... .... +(1/((2n−1)^2 ))−(1/((2n+1)^2 )) 2S_n =1−(1/((2n+1)^2 )) When n→∞S_n =1 =(1/2)ANS
$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\underset{{n}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\right\} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+….\right)−\left(\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{7}^{\mathrm{2}} }+…\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:{i}\:{made}\:{a}?{mistake}… \\ $$$$\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}×\mathrm{2}{n}×\mathrm{1}=\mathrm{8}{n} \\ $$$${but}\:{in}\:{problem}\:\frac{\mathrm{4}{n}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${so}\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\right\}\:{so}\:\frac{\mathrm{1}}{\mathrm{2}}\:{factor}\:{should} \\ $$$${be}\:{there}… \\ $$$${or}\:{methld} \\ $$$$\mathrm{2}{s}=\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} } \\ $$$$+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} } \\ $$$$…. \\ $$$$…. \\ $$$$+\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{2}{S}_{\boldsymbol{{n}}} =\mathrm{1}−\frac{\mathrm{1}}{\left(\mathrm{2}\boldsymbol{{n}}+\mathrm{1}\right)^{\mathrm{2}} }\:\:\:{When}\:{n}\rightarrow\infty{S}_{{n}} =\mathrm{1} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ANS} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *