Question Number 164240 by HongKing last updated on 15/Jan/22
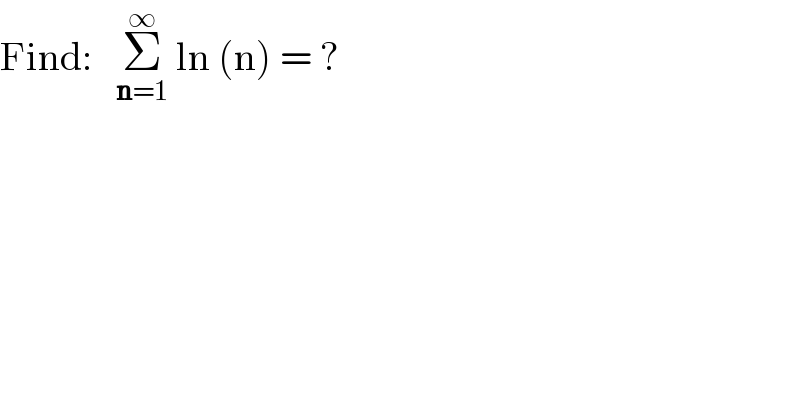
$$\mathrm{Find}:\:\:\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\mathrm{ln}\:\left(\mathrm{n}\right)\:=\:? \\ $$
Answered by mathmax by abdo last updated on 15/Jan/22
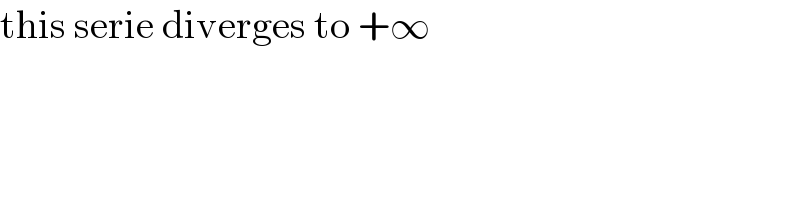
$$\mathrm{this}\:\mathrm{serie}\:\mathrm{diverges}\:\mathrm{to}\:+\infty \\ $$
Answered by alephzero last updated on 15/Jan/22
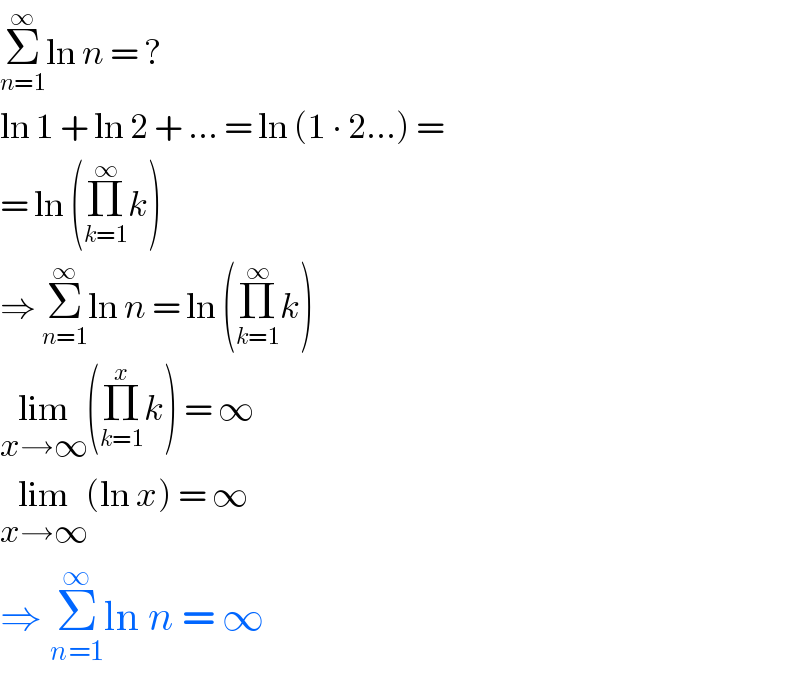
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{ln}\:{n}\:=\:? \\ $$$$\mathrm{ln}\:\mathrm{1}\:+\:\mathrm{ln}\:\mathrm{2}\:+\:…\:=\:\mathrm{ln}\:\left(\mathrm{1}\:\centerdot\:\mathrm{2}…\right)\:= \\ $$$$=\:\mathrm{ln}\:\left(\underset{{k}=\mathrm{1}} {\overset{\infty} {\prod}}{k}\right) \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{ln}\:{n}\:=\:\mathrm{ln}\:\left(\underset{{k}=\mathrm{1}} {\overset{\infty} {\prod}}{k}\right) \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\underset{{k}=\mathrm{1}} {\overset{{x}} {\prod}}{k}\right)\:=\:\infty \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{ln}\:{x}\right)\:=\:\infty \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{ln}\:{n}\:=\:\infty \\ $$
Commented by HongKing last updated on 15/Jan/22
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{dear}\:\mathrm{Sir} \\ $$
Commented by alephzero last updated on 16/Jan/22
$$\mathrm{You}\:\mathrm{are}\:\mathrm{welcome},\:\mathrm{Sir}. \\ $$
