Question Number 178543 by Acem last updated on 17/Oct/22
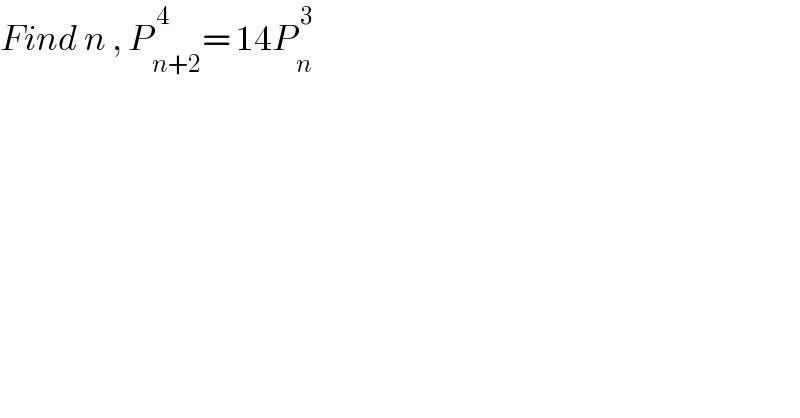
$${Find}\:{n}\:,\:{P}_{{n}+\mathrm{2}} ^{\:\mathrm{4}} =\:\mathrm{14}{P}_{{n}} ^{\:\mathrm{3}} \\ $$
Answered by Ar Brandon last updated on 18/Oct/22
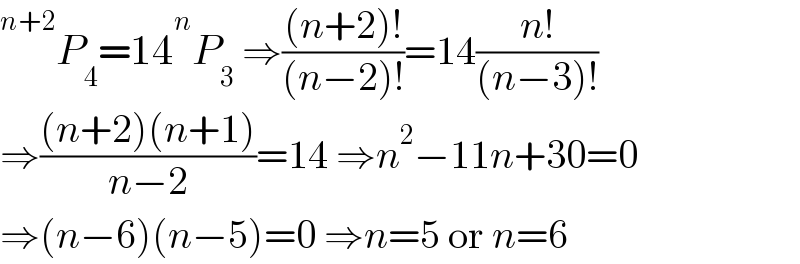
$$\overset{{n}+\mathrm{2}} {\:}{P}_{\mathrm{4}} =\mathrm{14}\overset{{n}} {\:}{P}_{\mathrm{3}} \:\Rightarrow\frac{\left({n}+\mathrm{2}\right)!}{\left({n}−\mathrm{2}\right)!}=\mathrm{14}\frac{{n}!}{\left({n}−\mathrm{3}\right)!} \\ $$$$\Rightarrow\frac{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right)}{{n}−\mathrm{2}}=\mathrm{14}\:\Rightarrow{n}^{\mathrm{2}} −\mathrm{11}{n}+\mathrm{30}=\mathrm{0} \\ $$$$\Rightarrow\left({n}−\mathrm{6}\right)\left({n}−\mathrm{5}\right)=\mathrm{0}\:\Rightarrow{n}=\mathrm{5}\:\mathrm{or}\:{n}=\mathrm{6} \\ $$
Commented by Acem last updated on 18/Oct/22

$${Very}\:{good}\:{Sir}! \\ $$
Commented by Acem last updated on 18/Oct/22

$$ \\ $$$${As}\:{an}\:{advice}\:{my}\:{friend},\:{we}\:{must}\:{find}\:{a}\:{condition} \\ $$$$\:{for}\:{n}\:{befor}\:{i}.{e}. \\ $$$$\left.\begin{matrix}{{P}_{\mathrm{4}} ^{\:{n}+\mathrm{2}} :\:{n}+\mathrm{2}\geqslant\:\mathrm{4}\:\Rightarrow\:{n}\geqslant\:\mathrm{2}}\\{{P}_{\mathrm{3}} ^{\:{n}} :\:{n}\geqslant\:\mathrm{3}}\end{matrix}\right\}\:\Rightarrow\:\boldsymbol{{n}}\geqslant\:\mathrm{3} \\ $$$$\:{After}\:{that}\:{we}\:{find}\:{n}\:{and}\:{accept}\:{only}\:{which} \\ $$$$\:{belonging}\:{to}\:{the}\:{domain}\:{above} \\ $$$$ \\ $$
Commented by Ar Brandon last updated on 18/Oct/22
You're right!
