Question Number 164810 by tabata last updated on 22/Jan/22

$${find}\:{n}^{{th}} \:{terms}\:{of}\:<\mathrm{1},\mathrm{0},\mathrm{1},\mathrm{0},\mathrm{1},\mathrm{0},….> \\ $$
Commented by mr W last updated on 22/Jan/22

$${a}_{{n}} ={n}\:\left({mod}\:\mathrm{2}\right) \\ $$$${a}_{{n}} =\frac{\mathrm{1}−\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}} \\ $$$$… \\ $$
Commented by Tawa11 last updated on 22/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by alephzero last updated on 24/Jan/22
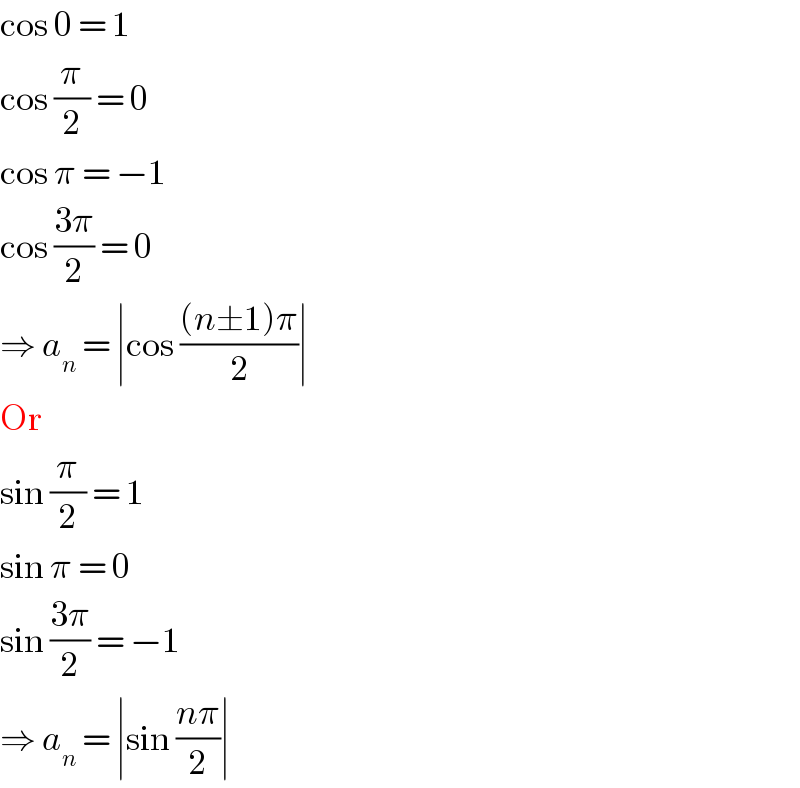
$$\mathrm{cos}\:\mathrm{0}\:=\:\mathrm{1} \\ $$$$\mathrm{cos}\:\frac{\pi}{\mathrm{2}}\:=\:\mathrm{0} \\ $$$$\mathrm{cos}\:\pi\:=\:−\mathrm{1} \\ $$$$\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{2}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{a}_{{n}} \:=\:\mid\mathrm{cos}\:\frac{\left({n}\pm\mathrm{1}\right)\pi}{\mathrm{2}}\mid \\ $$$$\mathrm{Or} \\ $$$$\mathrm{sin}\:\frac{\pi}{\mathrm{2}}\:=\:\mathrm{1} \\ $$$$\mathrm{sin}\:\pi\:=\:\mathrm{0} \\ $$$$\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{2}}\:=\:−\mathrm{1} \\ $$$$\Rightarrow\:{a}_{{n}} \:=\:\mid\mathrm{sin}\:\frac{{n}\pi}{\mathrm{2}}\mid \\ $$
