Question Number 52677 by maxmathsup by imad last updated on 11/Jan/19
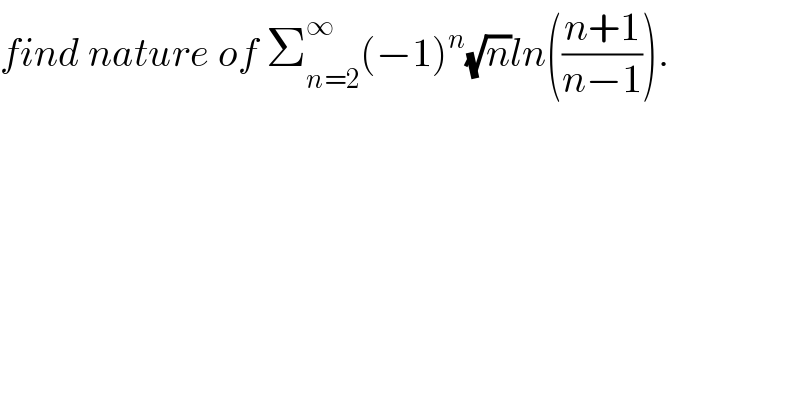
$${find}\:{nature}\:{of}\:\sum_{{n}=\mathrm{2}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \sqrt{{n}}{ln}\left(\frac{{n}+\mathrm{1}}{{n}−\mathrm{1}}\right). \\ $$
Commented by maxmathsup by imad last updated on 08/Feb/19
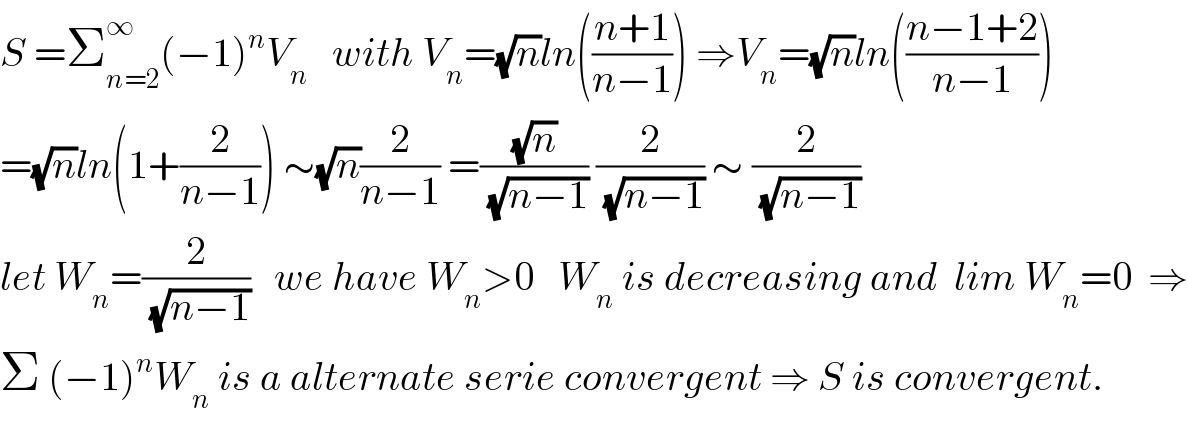
$${S}\:=\sum_{{n}=\mathrm{2}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {V}_{{n}} \:\:\:{with}\:{V}_{{n}} =\sqrt{{n}}{ln}\left(\frac{{n}+\mathrm{1}}{{n}−\mathrm{1}}\right)\:\Rightarrow{V}_{{n}} =\sqrt{{n}}{ln}\left(\frac{{n}−\mathrm{1}+\mathrm{2}}{{n}−\mathrm{1}}\right) \\ $$$$=\sqrt{{n}}{ln}\left(\mathrm{1}+\frac{\mathrm{2}}{{n}−\mathrm{1}}\right)\:\sim\sqrt{{n}}\frac{\mathrm{2}}{{n}−\mathrm{1}}\:=\frac{\sqrt{{n}}}{\:\sqrt{{n}−\mathrm{1}}}\:\frac{\mathrm{2}}{\:\sqrt{{n}−\mathrm{1}}}\:\sim\:\frac{\mathrm{2}}{\:\sqrt{{n}−\mathrm{1}}} \\ $$$${let}\:{W}_{{n}} =\frac{\mathrm{2}}{\:\sqrt{{n}−\mathrm{1}}}\:\:\:{we}\:{have}\:{W}_{{n}} >\mathrm{0}\:\:\:{W}_{{n}} \:{is}\:{decreasing}\:{and}\:\:{lim}\:{W}_{{n}} =\mathrm{0}\:\:\Rightarrow \\ $$$$\Sigma\:\left(−\mathrm{1}\right)^{{n}} {W}_{{n}} \:{is}\:{a}\:{alternate}\:{serie}\:{convergent}\:\Rightarrow\:{S}\:{is}\:{convergent}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Jan/19
![(T_n /T_(n−1) )=(((−1)^n )/((−1)^(n−1) ))×((√n)/( (√(n−1))))×((ln(((n+1)/(n−1))))/(ln(((n−1+1)/(n−1−1))))) =(−1)^1 ×(1/( (√(1−(1/n)))))×((ln(((1+(1/n))/(1−(1/n)))))/(ln((1/(1−(2/n)))))) =(−1)×1×((ln(((1+0)/(1−0))))/(ln((1/(1−0))))) [since n→∞] =−1×((ln1)/(ln1)) [here (0/0) is coming] if we cancell common N_r and D_r that is ln1 then given series is convergent... so others are requested to CHECk...](https://www.tinkutara.com/question/Q52724.png)
$$\frac{{T}_{{n}} }{{T}_{{n}−\mathrm{1}} }=\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }×\frac{\sqrt{{n}}}{\:\sqrt{{n}−\mathrm{1}}}×\frac{{ln}\left(\frac{{n}+\mathrm{1}}{{n}−\mathrm{1}}\right)}{{ln}\left(\frac{{n}−\mathrm{1}+\mathrm{1}}{{n}−\mathrm{1}−\mathrm{1}}\right)} \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{1}} ×\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{n}}}}×\frac{{ln}\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{{n}}}{\mathrm{1}−\frac{\mathrm{1}}{{n}}}\right)}{{ln}\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{2}}{{n}}}\right)} \\ $$$$=\left(−\mathrm{1}\right)×\mathrm{1}×\frac{{ln}\left(\frac{\mathrm{1}+\mathrm{0}}{\mathrm{1}−\mathrm{0}}\right)}{{ln}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{0}}\right)}\:\:\left[{since}\:{n}\rightarrow\infty\right] \\ $$$$=−\mathrm{1}×\frac{{ln}\mathrm{1}}{{ln}\mathrm{1}}\:\:\left[{here}\:\frac{\mathrm{0}}{\mathrm{0}}\:\:{is}\:{coming}\right] \\ $$$${if}\:{we}\:{cancell}\:{common}\:{N}_{{r}} \:{and}\:{D}_{{r}} \:{that}\:{is}\:{ln}\mathrm{1} \\ $$$${then}\:{given}\:{series}\:{is}\:{convergent}… \\ $$$${so}\:{others}\:{are}\:{requested}\:{to}\:\boldsymbol{{C}}{HECk}… \\ $$
