Question Number 90743 by abdomathmax last updated on 25/Apr/20
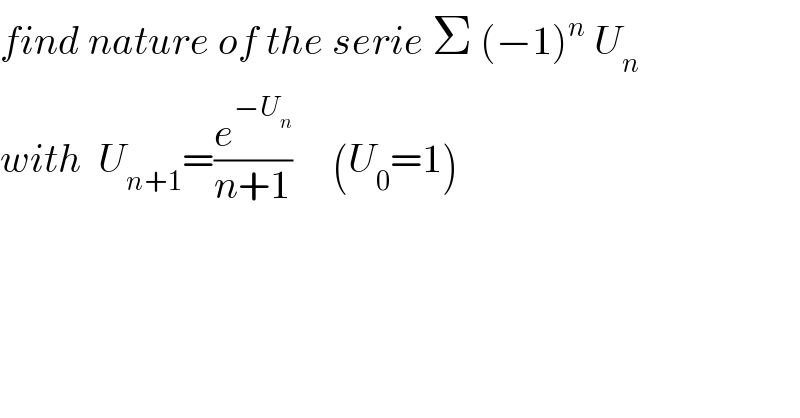
$${find}\:{nature}\:{of}\:{the}\:{serie}\:\Sigma\:\left(−\mathrm{1}\right)^{{n}} \:{U}_{{n}} \\ $$$${with}\:\:{U}_{{n}+\mathrm{1}} =\frac{{e}^{−{U}_{{n}} } }{{n}+\mathrm{1}}\:\:\:\:\:\left({U}_{\mathrm{0}} =\mathrm{1}\right) \\ $$
Answered by ~blr237~ last updated on 25/Apr/20
![we can show by induction that U_n ∈ ]0,1] so Σ(−1)^n U_n is an alternated serie then it converges if (U_n ) decrease and converges to zero. we have e^(−u_n ) <u_(n ) ; (1/(n+1))≤1 then u_(n+1) <u_n ∣u_n ∣≤(1/n) cause e^(−u_n ) <1 .so lim_(n→∞) u_n =0](https://www.tinkutara.com/question/Q90748.png)
$$\left.{w}\left.{e}\:{can}\:{show}\:{by}\:{induction}\:{that}\:\:{U}_{{n}} \in\:\right]\mathrm{0},\mathrm{1}\right] \\ $$$${so}\:\Sigma\left(−\mathrm{1}\right)^{{n}} {U}_{{n}} \:{is}\:{an}\:{alternated}\:{serie}\:{then}\:{it}\:{converges}\: \\ $$$${if}\:\left({U}_{{n}} \right)\:{decrease}\:{and}\:{converges}\:{to}\:\:{zero}. \\ $$$${we}\:{have}\:\:{e}^{−{u}_{{n}} } <{u}_{{n}\:} \:;\:\frac{\mathrm{1}}{{n}+\mathrm{1}}\leqslant\mathrm{1}\:\:{then}\:\:{u}_{{n}+\mathrm{1}} <{u}_{{n}} \: \\ $$$$\:\:\:\mid{u}_{{n}} \mid\leqslant\frac{\mathrm{1}}{{n}}\:\:{cause}\:\:{e}^{−{u}_{{n}} } <\mathrm{1}\:\:.{so}\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{u}_{{n}} \:=\mathrm{0} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 25/Apr/20

$${thankx}\:{sir} \\ $$
