Question Number 123672 by mathmax by abdo last updated on 27/Nov/20
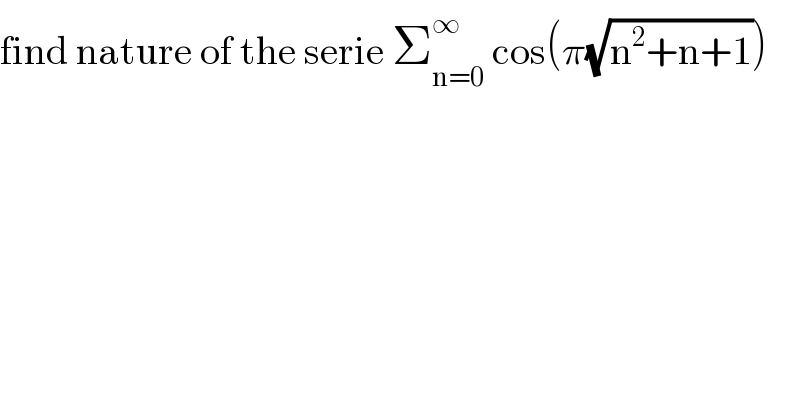
$$\mathrm{find}\:\mathrm{nature}\:\mathrm{of}\:\mathrm{the}\:\mathrm{serie}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\pi\sqrt{\mathrm{n}^{\mathrm{2}} +\mathrm{n}+\mathrm{1}}\right) \\ $$
Answered by mnjuly1970 last updated on 27/Nov/20
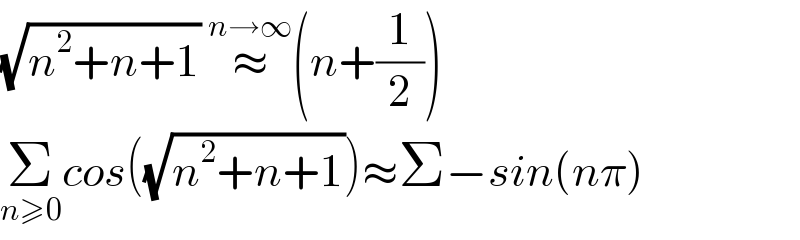
$$\sqrt{{n}^{\mathrm{2}} +{n}+\mathrm{1}}\:\overset{{n}\rightarrow\infty} {\approx}\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\underset{{n}\geqslant\mathrm{0}} {\sum}{cos}\left(\sqrt{{n}^{\mathrm{2}} +{n}+\mathrm{1}}\right)\approx\Sigma−{sin}\left({n}\pi\right) \\ $$
