Question Number 27785 by abdo imad last updated on 14/Jan/18
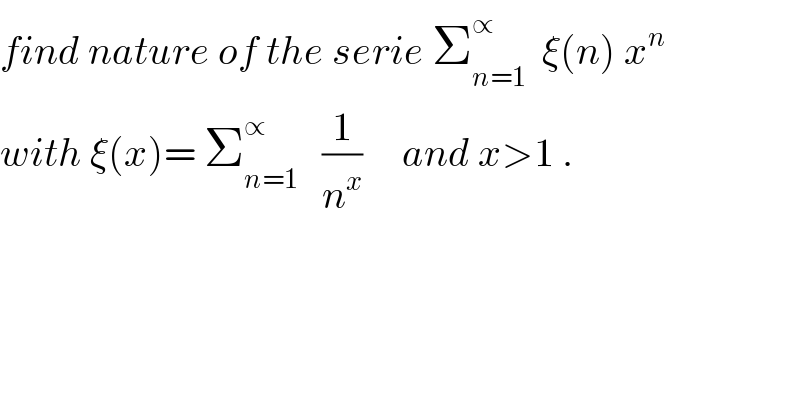
$${find}\:{nature}\:{of}\:{the}\:{serie}\:\sum_{{n}=\mathrm{1}} ^{\propto} \:\:\xi\left({n}\right)\:{x}^{{n}} \\ $$$${with}\:\xi\left({x}\right)=\:\sum_{{n}=\mathrm{1}} ^{\propto} \:\:\:\frac{\mathrm{1}}{{n}^{{x}} }\:\:\:\:\:{and}\:{x}>\mathrm{1}\:. \\ $$
Commented by abdo imad last updated on 20/Jan/18
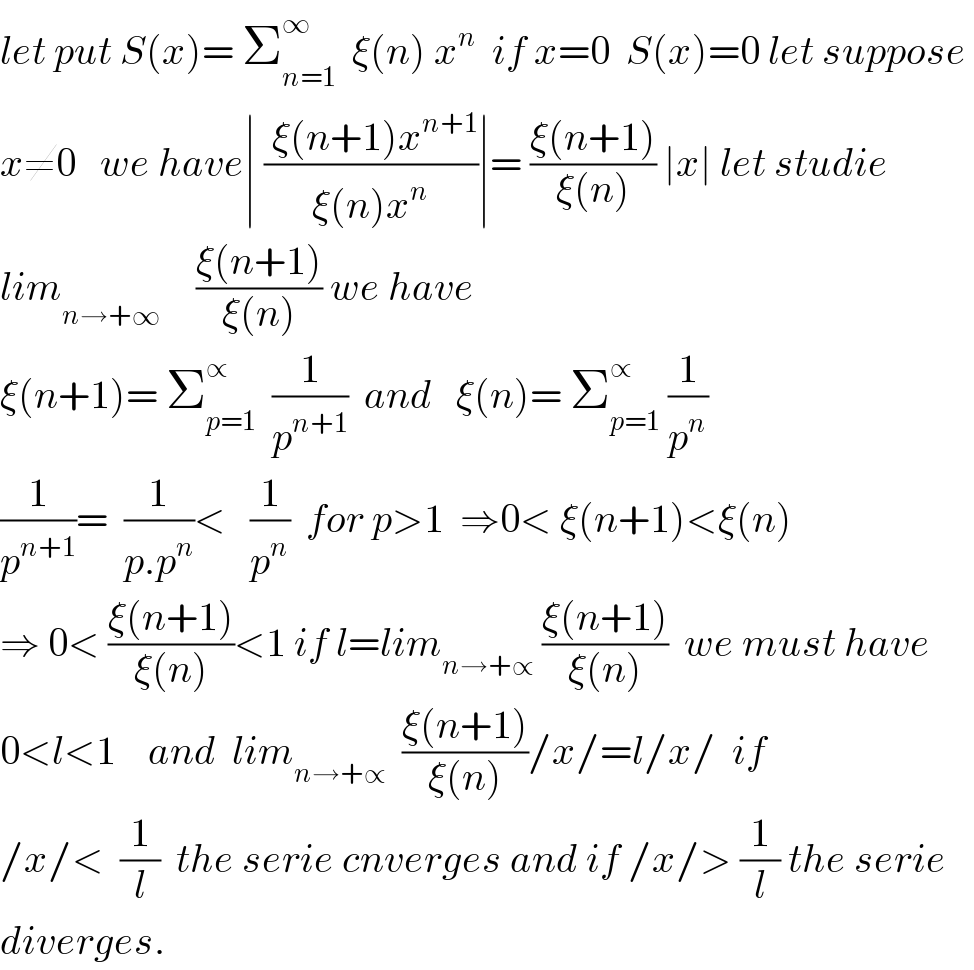
$${let}\:{put}\:{S}\left({x}\right)=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\xi\left({n}\right)\:{x}^{{n}} \:\:{if}\:{x}=\mathrm{0}\:\:{S}\left({x}\right)=\mathrm{0}\:{let}\:{suppose}\: \\ $$$${x}\neq\mathrm{0}\:\:\:{we}\:{have}\mid\:\frac{\:\xi\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{1}} }{\xi\left({n}\right){x}^{{n}} }\mid=\:\frac{\xi\left({n}+\mathrm{1}\right)}{\xi\left({n}\right)}\:\mid{x}\mid\:{let}\:{studie} \\ $$$${lim}_{{n}\rightarrow+\infty\:^{} } \:\:\:\frac{\xi\left({n}+\mathrm{1}\right)}{\xi\left({n}\right)}\:{we}\:{have} \\ $$$$\xi\left({n}+\mathrm{1}\right)=\:\sum_{{p}=\mathrm{1}} ^{\propto} \:\:\frac{\mathrm{1}}{{p}^{{n}+\mathrm{1}} }\:\:{and}\:\:\:\xi\left({n}\right)=\:\sum_{{p}=\mathrm{1}} ^{\propto} \:\frac{\mathrm{1}}{{p}^{{n}} } \\ $$$$\frac{\mathrm{1}}{{p}^{{n}+\mathrm{1}} }=\:\:\frac{\mathrm{1}}{{p}.{p}^{{n}} }<\:\:\:\frac{\mathrm{1}}{{p}^{{n}} }\:\:{for}\:{p}>\mathrm{1}\:\:\Rightarrow\mathrm{0}<\:\xi\left({n}+\mathrm{1}\right)<\xi\left({n}\right) \\ $$$$\Rightarrow\:\mathrm{0}<\:\frac{\xi\left({n}+\mathrm{1}\right)}{\xi\left({n}\right)}<\mathrm{1}\:{if}\:{l}={lim}_{{n}\rightarrow+\propto} \:\frac{\xi\left({n}+\mathrm{1}\right)}{\xi\left({n}\right)}\:\:{we}\:{must}\:{have} \\ $$$$\mathrm{0}<{l}<\mathrm{1}\:\:\:\:{and}\:\:{lim}_{{n}\rightarrow+\propto} \:\:\frac{\xi\left({n}+\mathrm{1}\right)}{\xi\left({n}\right)}/{x}/={l}/{x}/\:\:{if} \\ $$$$/{x}/<\:\:\frac{\mathrm{1}}{{l}}\:\:{the}\:{serie}\:{cnverges}\:{and}\:{if}\:/{x}/>\:\frac{\mathrm{1}}{{l}}\:{the}\:{serie} \\ $$$${diverges}. \\ $$
