Question Number 29140 by mathshooter last updated on 04/Feb/18
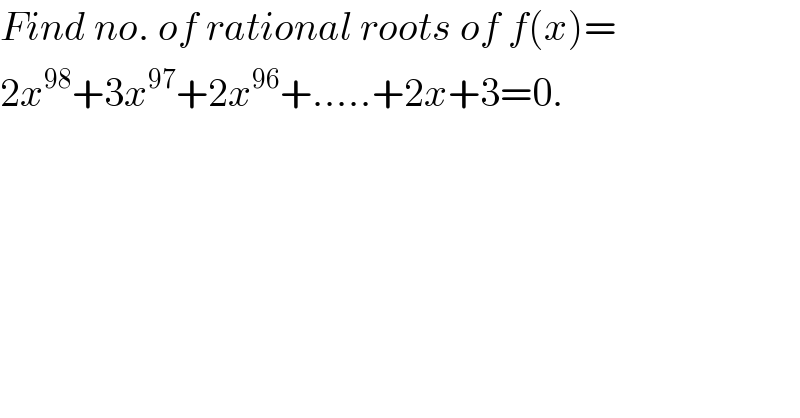
$${Find}\:{no}.\:{of}\:{rational}\:{roots}\:{of}\:{f}\left({x}\right)= \\ $$$$\mathrm{2}{x}^{\mathrm{98}} +\mathrm{3}{x}^{\mathrm{97}} +\mathrm{2}{x}^{\mathrm{96}} +…..+\mathrm{2}{x}+\mathrm{3}=\mathrm{0}. \\ $$
Commented by math solver last updated on 05/Feb/18
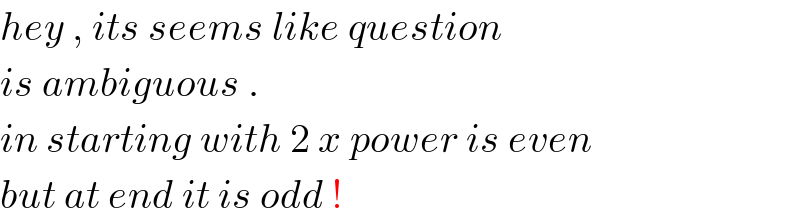
$${hey}\:,\:{its}\:{seems}\:{like}\:{question}\: \\ $$$${is}\:{ambiguous}\:. \\ $$$${in}\:{starting}\:{with}\:\mathrm{2}\:{x}\:{power}\:{is}\:{even}\: \\ $$$${but}\:{at}\:{end}\:{it}\:{is}\:{odd}\:! \\ $$
Commented by math solver last updated on 05/Feb/18
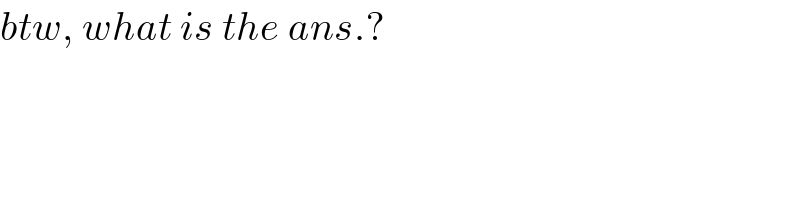
$${btw},\:{what}\:{is}\:{the}\:{ans}.? \\ $$
Commented by mathshooter last updated on 05/Feb/18

$$−\mathrm{1}\:\:{and}\:−\frac{\mathrm{3}}{\mathrm{2}}. \\ $$
Commented by mathshooter last updated on 05/Feb/18
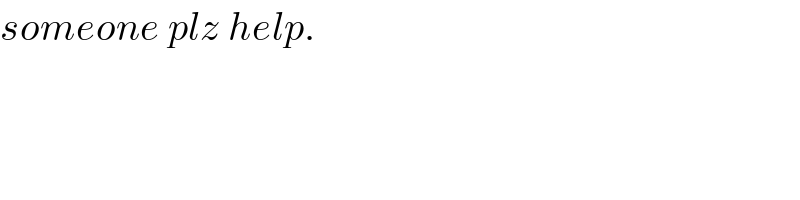
$${someone}\:{plz}\:{help}. \\ $$
Commented by math solver last updated on 07/Feb/18

$${yes}\:{sir}. \\ $$$${q}.\:{is}\:{wrong}. \\ $$
Commented by mrW2 last updated on 06/Feb/18

$${the}\:{function}\:{f}\left({x}\right)\:{is}\:{not}\:{clearly}\:{defined}. \\ $$
