Question Number 41705 by abdo.msup.com last updated on 11/Aug/18
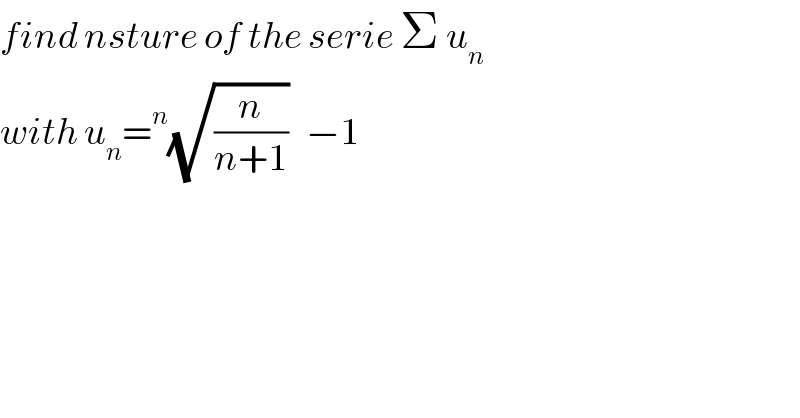
$${find}\:{nsture}\:{of}\:{the}\:{serie}\:\Sigma\:{u}_{{n}} \\ $$$${with}\:{u}_{{n}} =^{{n}} \sqrt{\frac{{n}}{{n}+\mathrm{1}}}\:\:\:−\mathrm{1} \\ $$
Commented by maxmathsup by imad last updated on 12/Aug/18
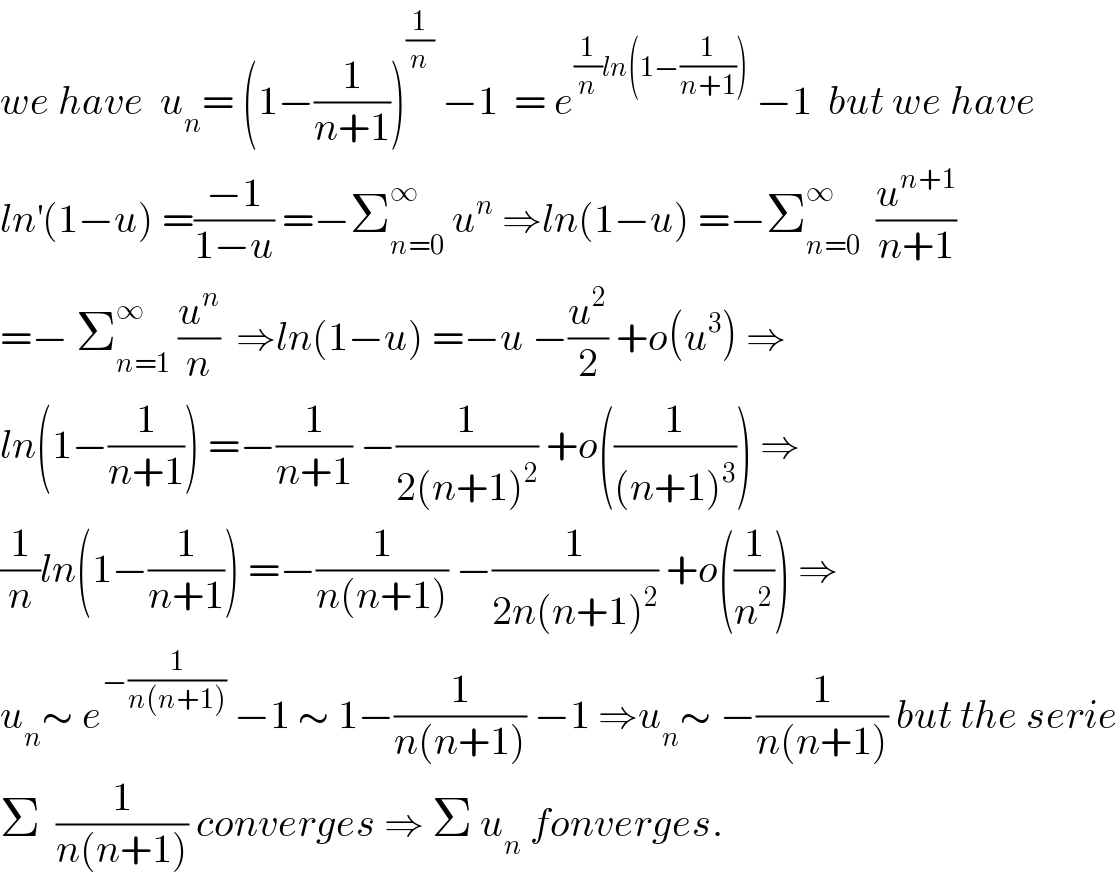
$${we}\:{have}\:\:{u}_{{n}} =\:\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)^{\frac{\mathrm{1}}{{n}}} \:−\mathrm{1}\:\:=\:{e}^{\frac{\mathrm{1}}{{n}}{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)} \:−\mathrm{1}\:\:{but}\:{we}\:{have} \\ $$$${ln}^{'} \left(\mathrm{1}−{u}\right)\:=\frac{−\mathrm{1}}{\mathrm{1}−{u}}\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:{u}^{{n}} \:\Rightarrow{ln}\left(\mathrm{1}−{u}\right)\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{u}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}} \\ $$$$=−\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{u}^{{n}} }{{n}}\:\:\Rightarrow{ln}\left(\mathrm{1}−{u}\right)\:=−{u}\:−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({u}^{\mathrm{3}} \right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)\:=−\frac{\mathrm{1}}{{n}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:+{o}\left(\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{3}} }\right)\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{{n}}{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)\:=−\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$${u}_{{n}} \sim\:{e}^{−\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}} \:−\mathrm{1}\:\sim\:\mathrm{1}−\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}\:−\mathrm{1}\:\Rightarrow{u}_{{n}} \sim\:−\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}\:{but}\:{the}\:{serie} \\ $$$$\Sigma\:\:\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}\:{converges}\:\Rightarrow\:\Sigma\:{u}_{{n}} \:{fonverges}. \\ $$
